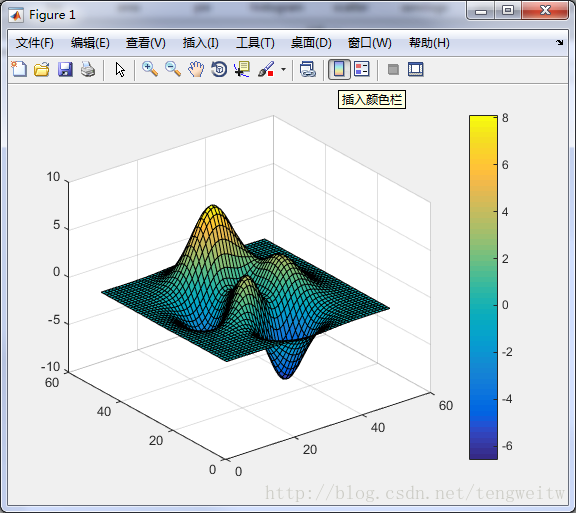
画过图的都知道，我们常常用颜色的深浅来表示值的大小，在Matlab作图中，我们使用的是colorbar这个函数来给出颜色的直观参考。下面给出Matlab的示例：在Matlab命令窗口输入：

1
2
3
4
5

figure

surf(peaks)

colorbar

可以得到的图像如下：

昨天是清明节，也是复活节。清明节我是知道的，就是祭祖扫墓的日子。复活节我就听说过，谷歌了一下：复活节是西方基督教徒纪念他们的上帝之子耶稣死后三天复活的节日，一个纯粹的宗教节日，象征重生与希望。比较有趣的是，今年中国的清明节与西方的复活节意外相遇，而去年中国的元宵节与西方的情人节不期而至。想想，这两两节日之间也是有联系的。

去年暑假的时候，作为学习Qt的实战，我写了一个名为《我爱查词典》的词典软件。后来由于导师项目及上课等原因，时间不足，所以该软件的部分功能欠缺，性能有待改善。这学期重新拿出来看时，又有很多东西都不熟悉了。恰逢这学期课比较少，于是乎想写写关于这个软件制作的一系列文章，对日后重拾该软件时能够较快入手。当然，也非常乐意读者们在该软件的基础上添加一些功能，源代码会在该系列文章写完之后公布。可运行的词典软件的下载地址：http://download.csdn.net/detail/tengweitw/8548767

对于一个没有考过研的人来说，谈考研好像有点不着边际。正如韩寒导演的电影《后会无期》中的一句台词：你连世界都没观过，哪来的世界观。不过古语有云：当局者迷，旁观者清。我就以一个旁观者的身份来谈谈考研。（以下内容都是我本人的观点，与我本人无关—皆为自己的妄言之言）

八皇后问题是一道经典的回溯问题。问题描述如下：皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上（有8*8个方格），使它们谁也不能被吃掉？

看到这个问题，最容易想到的就是遍历穷举法，不过仔细一想，思路虽然非常清晰，但是需要遍历次数太多，时间复杂度很高。那么，我们应该怎么办呢？下面给出算法思路：

算法思想：首先尝试在第一行放置第一个皇后，然后在第二行放置第二个使之与前面的皇后不构成威胁，依此类推。如果发现不能放置下一个皇后，就回溯到上一步，试着将皇后放在其他的位置。最后，或者尝试完所有的可能或者找到解决方案。

这种算法思想与中国的一句古话“不撞南墙不回头”类似：一路向前走，直到走到死胡同，然后往回走，回到上一个岔路口，重新选择一个方向，继续向前走，直到到达目的地。

离过年都不到十天了，还要等到这周五才能回家，想想也一年没回家了。从寒假开始到现在，已经有二十来天，这期间把2014年总结中的寒假计划也大多数完成了：The Element Of Style的阅读，三门数学课《随机过程》、《工程优化》、《数值分析》的算法实现。回家过年期间肯定不会写博客了，今天一看，这个月只写了三篇，于是乎今天必须再写一篇来完成这个月的基本工作量。言归正传，这篇文章写写选修课《算法设计》作业题中的矩阵乘法的三种方法。

牛顿法

使用条件：目标函数具有二阶导数，且海塞矩阵正定。

优缺点： 收敛速度快、计算量大、很依赖初始点的选择。

算法的基本步骤：

已知目标函数$f(x)$，梯度$g(x)$, Hessan矩阵$G(x)$, 给定误差限$\epsilon$:

• 步骤1：选定初始点$x_0$，计算$f_0=f(x_0), k=0$;
• 步骤2：计算$g_k=g(x_k)$，如果$\Vert g_k\Vert\le\epsilon$, 算法停止, $x^\star=x_k$，否则转到步骤3：
• 步骤3：计算$G_k=G(x_k)$, 由方程$G_kd^k=-g_k$, 解得$d^k$;
• 步骤4：令$x_{k+1}=x_k+d^{k}, k=k+1$, 转到步骤2

算法流程图：

​

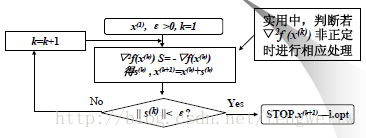
一维搜索方法的分类如下：

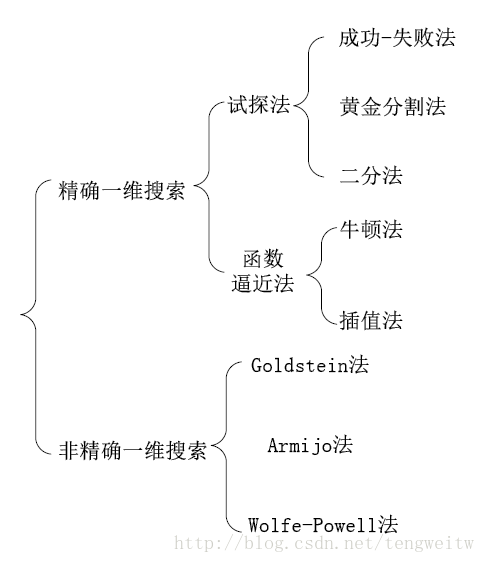
这篇文章主要讲解黄金分割法、二分法、牛顿法这三种一维搜索方法。黄金分割法只用到原函数，二分法用到函数的一阶导，牛顿法用到函数的二阶导。由于本文主要对研一上学期的课程中的部分算法进行程序实现，理论部分大多参考上课的课件。

对于积分$\int_{a}^{b}f(x)dx$只要找到被积公式的原函数$F(x)$，利用牛顿莱普利兹公式有：

但是，实际使用这种求积分的方法往往是有困难的，因为大量的被积函数的原函数是不能用初等函数表示的；另外，当$f(x)$是由测量或数值计算给出的一张数据表时，牛顿莱普利兹公式也无法直接运用，因此有必要研究积分的数值计算问题。

在2014年终总结中，我提到要对这学期学过的数学课中的部分算法进行仿真实现。《数值分析》和《工程优化》这两门数学课里面还有些专门讲算法的，可以用来仿真。在《随机过程》这门课中，几乎全都是公式推导，定理证明，实在难以仿真实现。最后发现，马尔科夫链这一章比较适合仿真，况且先前也写过类似的程序，更重要的是之前有人也问过关于马氏链的Matlab实现问题。关于马氏链的理论原理在这就不作描述，下面直接用程序来实现具体问题的求解。