QApplication类和QWidget类都包含在QtGui模块中。所以我们可以只包含这个头文件即可。
在c++中,用new分配了内存空间就需要用delete来释放空间,而在Qt中,释放父对象时,会自动销毁子对象。
将光标定位到函数上时,会浮现出提示,按提示按f1就可以进入该函数的帮助文档。
在main.c文件中,程序只有进入了主事件循环后才能接受事件,而show函数会触发显示事件,所以只有在完成a.exe()函数调用进入消息循环后才能正常显示。
使用qDebug(“x:%d”,x)不需要添加
头文件的。使用qDebug<<x则需要包含该头文件。 按照运行对话框时,是否还可以和该程序的其它窗口进行交互,可以分为模态和非模态。
在一个函数中定义的变量,等这个函数执行结束后,就自动释放内存了。因此我们一般将子部件定义为指针类型。
要想使一个对话框成为模态对话框,只需要调用它的exec()函数,而要使其成为非模态对话框,可以使用new操作来创建,然后使用show()函数来显示。
信号和槽都是函数,信号只需声明不需要定义。
信号和槽的关联可以分为自动关联和手动关联。自动关联就是使用规定的槽命名,而且必须使用Qt部件已经提供的信号。
快捷更改函数名:在函数上右击,选择重构->Rename Symbol Under Cursor
Qt 设计器直接生成的槽是自动关联,我们必须在调用setupUi()函数前定义子部件和对象名。因为setupUi调用connectSlotsByName()函数用来支持信号和槽的自动关联,调用时需要使用对象名。
信号和槽的特点:类型是安全的、松耦合的、参数灵活、比回调机制稍慢。
行编辑器的属性栏中还可以设置占位符,就是没有输入信息前的一些提示语句,就是更改编辑器的placeholderText属性。
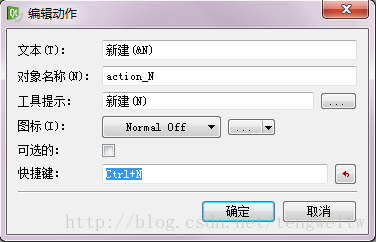
加速键与快捷键的不同之处:如下图:我们设置’’新建’’的快捷键为
ctrl+N,加速键为N,那么我们可以按下ctrl+N来新建文件,也可以先按alt+F激活’’文件’’菜单,然后按N来新建文件。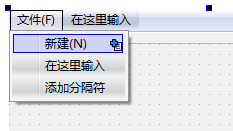
【Matlab编程】Matlab版扫雷
本文字数: 7.1k 阅读时长 ≈ 10 分钟
我发现有些人平常闲着的时候会玩window自带的游戏,其中最常见的就是扫雷和纸牌。本来想用matlab编写全自动扫雷程序用来作弊,可是后来发现扫雷问题是NP完全问题(正如:旅行商NP难问题一样不能被解决),便放弃了。于是编写了类似扫雷游戏(没有经过大量测试,可能有bug,效率也不高,作弊:在命令窗口输入minefield 其中,值为1的地方为雷区)。大致规则和原来一样,只是做了些改进:加入了音乐和语音提示。具体代码如下(下面有两个文件:一个脚本文件,一个函数文件,只需运行第一个脚本文件即可):
【Qt编程】Qt学习笔记
本文字数: 1.1k 阅读时长 ≈ 2 分钟
在创建项目时,项目名和路径中都不能出现中文。
可以使用
Ctrl + “+”和Ctrl + “-”来改变程序的字体大小(Ctrl+鼠标滑轮可达到同样效果),使用Ctrl + “0”可以恢复到默认字体大小。在设计模式下有几个过滤器,就是写着
Filter的行输入框,可以帮助你更快的找到所需要的部件。如果生成的.exe文件不能运行,并且提示丢失.dll文件,可以按照提示在Qt的安装目录的bin目录下寻找这些.dll文件。还有一种一劳永逸的方法是:将Qt的安装目录的bin目录加到系统的Path环境变量中去,这样程序运行是就可以自动找到那些dll文件。
在Qt Creator 默认下,编译的程序要想发布就需要dll文件,这种编译方式就称为动态编译。静态编译是指将Qt 的库进行重新编译,发布时不需要dll文件.
设置应用程序的图标:
- 将myico.ico(名字可以自己取)图标文件放入工程的目录下,在目录里建立文本文档并写入下面代码
IDI_ICON1 ICON DISCARDABLE"myico.ico"然后将该文本文档改为myico.rc (注意更改后缀名) - 在项目文件中的pro文件中的最后添加下面代码:
RC_FILE += myico.rc
- 将myico.ico(名字可以自己取)图标文件放入工程的目录下,在目录里建立文本文档并写入下面代码
任何一个QtGUI都需要一个QApplication类对象来管理应用程序的资源。
在默认情况下,新建的可视部件对象是不可见的,我们可以通过
show()来显示。中文显示乱码的解决办法:
1
QTextCodec::setCodecForTr(QTextCodec::codecForName("UTF-8")); QTextCodec::setCodecForTr(QTextCodec::codecForLocale());
在Windows系统下,其中一个能正常显示,最好两者都写上。
Qt Creator的代码补全功能
当输入一个比较长得函数或变量名时,可以通过其中的几个字母来定位。比如说,要输入前面讲到的setFocus()函数,那么只需输入首字母s和后面的大写字母F即可,这样可以大大缩减提示列表,如果还没有定位到,那么可以输入F后面的字母。如下图1所示。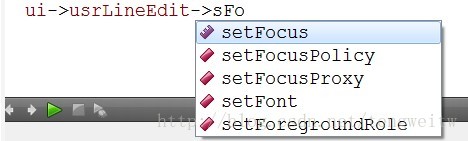
默认的情况下,对话框的左上角是(0,0)。
Ui文件生成的默认头文件的名称是ui_加ui文件的名称;ui文件是使用uic编译工具来编译的。
当有多个项目并存时,我们可以在项目文件右击来设定活动项目。
在项目发布时,不需要包含user文件,如果要打开别人的项目文件,我们应该去掉这种类型的文件。
我们可以将pro文件直接拖向Qt Creator图标来打开项目。
【算法导论】我的2013--一切从心开始
本文字数: 5.2k 阅读时长 ≈ 7 分钟
【算法导论】最大二分匹配
本文字数: 3.2k 阅读时长 ≈ 5 分钟
最大二分匹配问题在现实生活中比较普遍,常常出现在任务分配上。例如,有5个员工,4个不同的任务,而不同员工能够完成不同或相同的任务。也就是说,有的员工只会做这个任务,有的员工会做那个任务,有的员工会做一些任务。图解如下:左边代表员工,右边代表任务,连线代表有能力完成。
【算法导论】最大流算法
本文字数: 5.2k 阅读时长 ≈ 7 分钟
最大流问题就是在容量容许的条件下,从源点到汇点所能通过的最大流量。
流网络
网络流G=(v, E)是一个有向图,其中每条边(u, v)均有一个非负的容量值,记为c(u, v) ≧ 0。如果(u, v) ∉ E则可以规定c(u, v) = 0。网络流中有两个特殊的顶点,即源点s和汇点t。
与网络流相关的一个概念是流。设G是一个流网络,其容量为c。设s为网络的源点,t为汇点,那么G的流是一个函数f:V×V →R,满足一下性质:
- 容量限制:对所有顶点对u,v∈V,满足f(u, v) ≦ c(u, v);
- 反对称性:对所有顶点对u,v∈V,满足f(u, v) = - f(v, u);
- 流守恒性:对所有顶点对u∈V-{s, t},满足Σv∈Vf(u,v)=0。
本文开始讨论解决最大流问题的Ford-Fulkerson方法,该方法也称作“扩充路径方法”,该方法是大量算法的基础,有多种实现方法。
【算法导论】幻方算法
本文字数: 4.5k 阅读时长 ≈ 6 分钟
说起幻方,大家应该在小学时候就已经接触过了,最简单的就是九宫格,射雕英雄传中的那段至今还记得:戴九履一,左三右七,二四为肩,六八为足。下面我们就来看看这个有趣的问题。
【算法导论】地图染色算法
本文字数: 1.2k 阅读时长 ≈ 2 分钟
地图染色问题可以根据四色定理来解决。所谓四色定理,就是指可以用不多于四种的颜色对地图着色,使相邻的行政区域不重色,因此我们可以用四色定理的结论,用回溯算法对一幅给定的地图染色。
算法的基本思想是:从第(1)号行政区域开始染色,每个区域逐次用颜色1#、2#、3#、4#进行试探,若当前所取的颜色与周围已染色的行政区域不重色,则用栈记下该区域的颜色序号,否则依次用下一颜色进行试探;若出现用1#到4#颜色均与相邻区域的颜色重色,则需退栈回溯,修改当前栈顶的颜色序号,再进行试探。直到所有行政区域都已分配合适的颜色。
【算法导论】有向图的可达矩阵
本文字数: 1.6k 阅读时长 ≈ 2 分钟
有时候,我们关注的不是从一个地点到另一个地点的费用,而是能否从一个顶点到达另一个顶点。因此我们可以假设所有边的权值为单位1,在下面的算法中,我们可以在$O(n^3)$的时间内计算出图中任意两点是否可达,我用可达矩阵来表示有向图中两者是否可达。如果可以从$i$到$j$,则定义$t{ij}=1$,否则$t{ij}=0$。因此我们可以得到下式:

我们以下面的有向图进行具体实现:
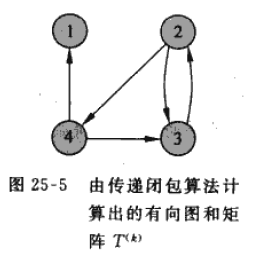
下图给出了计算所得的每一个$T^{(k)}$矩阵:
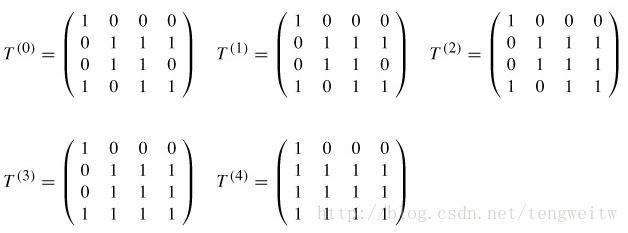
具体程序实现如下:
1 | #include<stdio.h> |
在上面的程序中,我用了逻辑运算来计算可达矩阵,因为在某些计算机上,对单位的值,逻辑操作的执行速度快于对整数字长数据的算术运算操作,其空间要求也比整数要小。
学过图论的可能知道,一个邻接矩阵$A$(若边的权值都为单位$1$)表示两个顶点经过一步的可达情况, $A{ij}$表示经过一步,$i$能到达$j$的次数。同理$A^{(2)}$表示两个顶点经过两部步的可达情况,$A{ij}$表示经过两步,$i$能到达$j$的次数,一次类推……。还是以上面的图为例:
比如$A^{(2)}$中$A_{12}=2$,表示从顶点$2$到顶点$3$经过两步可以到达的次数为$3$。 注意:自己到达自己可以是任意步!
由相关知识可知,可达矩阵$B=A+A^{(2)}+A^{(3)}+\cdots+A^{(n)}$ ,$n$为顶点个数。具体的C语言实现比上面的算法要复杂,下面用matlab实现:
1 | function P = canget( A ) |
结算可以得到相同的结果。由于matlab擅长矩阵运算,因此程序计算十分简单。
【算法导论】每对顶点之间的最短路径算法
本文字数: 2.2k 阅读时长 ≈ 3 分钟
对于一个顶点数为N的有向网路图,我们可以通过前面所提到的单源最短路径算法执行N次来获得每一对顶点间的最短路径。这种方法的时间复杂度为$O(N^3)$。如果网络中有负权值的边,则需要使用前面提到的单源最短路径算法之Bellman—Floyd算法。总之,总可以通过单源最短路径来求得每对顶点间的最短路径。这里我就不再用程序实现上述方法。下面介绍Floyd解决这一问题的另一种算法,它形式简单,利于理解,而且时间复杂度同样为$O(N^3)$。