0%

【概率统计】连续分布的产生

发表于 更新于
本文字数： 7.2k 阅读时长 ≈ 10 分钟

由于篇幅有限，前一篇文章《离散分布的产生》中只讲述了用均匀分布产生离散分布的方法，那么本文接着讲如何利用均匀分布产生连续分布的方法。

连续分布主要有以下几种：均匀分布 伽马分布 正态分布 贝塔分布 柯西分布 对数正态分布 双指数分布。

产生各种连续分布的方法有很多，我把它分为两类：通用方法、特殊方法。特殊方法就是根据各个连续分布的特性而特有的方法。

通用方法

通用方法指的是对于各种连续分布理论上都适用的方法。下面只讲解分布函数法、舍取法这两种通用的方法。

分布函数法

概率积分变换定理
设随机变量$X$有连续累计分布函数$F(x)$，令$U=F(X)$，则$U$服从$(0,1)$上的均匀分布。

由概率积分变换定理可知，如果知道一个连续分布函数的累计分布函数$F(x)$，则可以求得随机变量：$X=F^{-1}(U)$，其中$U$服从$0$到$1$内的均匀分布。下面以指数分布来举例说明：
指数分布的累计分布函数$F(x)$可以表示为：

由于$U=F(X)$服从$(0,1)$上的均匀分布，则随机变量：$X=F^{-1}(U) = - \frac{Ln\left( 1 - U \right)}{\lambda }$。因此只需要产生服从$(0,1)$上的均匀分布的$U$，就可以计算得到服从指数分布的随机变量$X$。

  • 指数分布　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
%指数分布
%参数：到达率lambda
%mean=1/lamda,  var=1/lambda^2
clear all
close all
clc
lambda=1;%指数分布的产生lambda
n=10;%x的取值为0到无穷大，这里只取前n个

%------------------------由内置函数直接给出-------------------------%

%指数分布的产生，即事件发生的时间间隔x,x取值为0到正无穷
X=exprnd(1/lambda);%产生1均值为1/lamda的指数分布

%指数分布的cdf
x=0:.1:n;
Fx=expcdf(x,1/lambda);
%figure
%plot(x,Fx,'-')
%title('指数分布的cdf')

%指数分布的pdf
x=0:.1:n;
Px=exppdf(x,1/lambda);
figure
plot(x,Px,'r-')
hold on
title('指数分布的pdf')



%-------------------------由均匀分布推导出（分布函数法）-------------------------%
N=1000;%样本点数
U=rand(1,N);%U服从均匀分布

X2=-(log(1-U))/lambda;%X2服从指数分布，X2由分布函数法得到，对于不同的分布，分布函数不同，这里的表达式需作相应的改变！

%下面的程序是绘制X2的概率密度函数pdf
Max=ceil(max(X2));
step=1;%步长
range=0:step:Max;

for i=1:length(range)-1
    YY(i)=sum(range(i)<=X2&X2<=range(i+1))/N/step;%统计落在区间中的点数
    XX(i)=(range(i)+range(i+1))/2;
end

plot(XX,YY,'bo')
hold on
title('指数分布的pdf')
legend('内置函数产生','分布函数法产生')

结果显示如下：(指数参数$\lambda=1$的情况)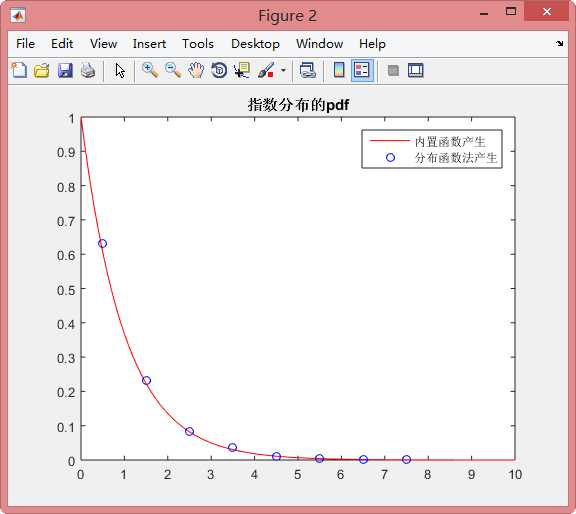
图1

分布函数法的局限性：由于该方法的关键就是求出分布函数的反函数，从而得到随机变量$X$关于均匀分布随机变量$U$的表达式。然而有些分布是不容易求得其反函数的，例如我们常见的正态分布，其分布函数需要用其概率密度函数表示如下：

其中，$u$和$\sigma$分布为均值和标准差。显然，当得知$F(x)$的取值时，也很难求得此时的$x$的值。因此，当出现上述问题时，我们可以采用舍去法。

舍去法

定理：设随机变量$Y,V$的概率密度函数分布为$f{Y}(y)、f{V}(v)$，其中，$f{Y}(y)、f{V}(v)$有相同的支撑集且
$M =\max\left{f{Y}(y)/f{V}(v)\right} < + \infty $
*按下列步骤可以生成随机变量$Y$服从概率密度为$f_{Y}(y)$的分布：*

  1. 生成独立的随机变量$U,V$，其中，$U$服从$0$到$1$的均匀分布,$V$服从概率密度函数为$f_{V}(v)$的分布
  2. 如果$U <\frac{1}{M}f{Y}(V)/f{V}(V)$,则令$Y=V$，否则返回到步骤1。

下面以用舍去法生成正态分布来具体说明：假设我们要用舍取法生成标准正态分布，标准正态分布的概率密度函数如下所示：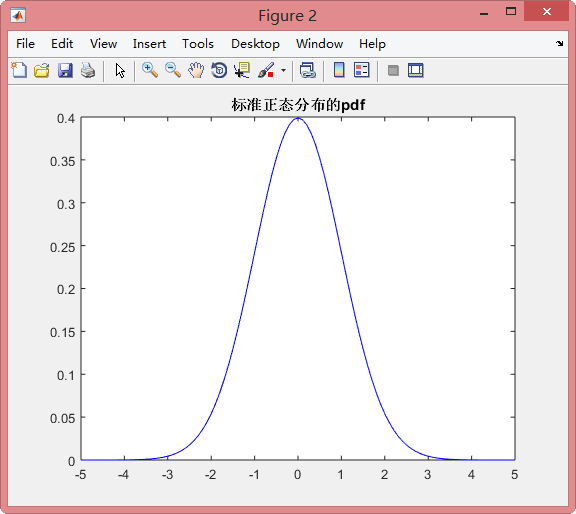
图2

  • 确定$V$的分布
    由舍取法的步骤2可知，生成的正态分布变量$Y$的取值包含于随机变量$V$的取值中。因此，我们需要根据正态分布随机变量的取值范围，来选择$V$应该服从的分布！我们一般取$V$服从均匀分布（当然也可以取其他的分布，注意需要满足取值范围）。
    理论上，正态随机变量的取值在整个实数域中，因此$V$应该服从区间为实数域的均匀分布，显然这个均匀分布我们很难表示出来。但由上图可知，标准正态分布的取值基本在$-5$到$5$之间，因此我们只需要使得$V$服从区间在$-5$到$5$的均匀分布即可以很好的近似。

  • 确定$M$的大小
    在公式$M =\max\left{f{Y}(y)/f{V}(v)\right} $中，${fV}(v) = \frac{1}{10}$，$\max\left{f{Y}(y)\right} =f_{Y}(0)=\frac{1}{\sqrt {2\pi } }$。因此$M=\frac{10}{\sqrt {2\pi } }$

在确定了$V$的分布以及$M$的大小之后，便可以根据定理中步骤2的判决方法来生成服从指定分布的随机变量$Y$。具体的程序实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
%-------------------正态分布-----------------------%
%参数：均值mu，方差sigma2
%mean=mu,  var=sigma2
clear all
close all
clc
mu=0;
sigma2=1;
n=10;%x的取值为正负无穷大，
%-------------------由内置函数直接给出----------------%
%正态分布的产生X
X=normrnd(mu,sqrt(sigma2));%产生均值mu，方差sigma2的正态分布

%正态分布的cdf
x=0:.1:n;
Fx=normcdf(x,mu,sqrt(sigma2));
% figure
% plot(x,Fx,'-')
% title('正态分布的cdf')

%指数分布的pdf
x=-5:.1:5;
Px=normpdf(x,mu,sqrt(sigma2));
figure
plot(x,Px,'b-')
hold on

%------由舍选法推导出--------%

N=100;
A=-5;%A,B位均匀分布的取值区间
B=5;

i=1;
while(i<=N)
    U=unifrnd(0,1);%服从（0,1）的均匀分布
    V=unifrnd(A,B);%服从（A,B）的均匀分布
    M=1/sqrt(2*pi)*(B-A);%计算得到M
    if(U<1/M*1/sqrt(2*pi*sigma2)*exp(-(V-mu)^2/2/sigma2));%由定理得到的公式来生成随机变量X2
        X2(i)=V;%X2就是我们要生成的指定分布的随机变量
        i=i+1;
    end  
end

%下面的程序是计算通过舍去法生成的正态分布X2的pdf
Max=ceil(max(X2));
step=1;
range=A:step:B;

for i=1:length(range)-1
    YY(i)=sum(range(i)<=X2&X2<=range(i+1))/N/step;
    XX(i)=(range(i)+range(i+1))/2;
end

plot(XX,YY,'ro')
hold on
title('正态分布的pdf')
legend('内部函数产生','舍取法产生')

结果显示如下：
图3

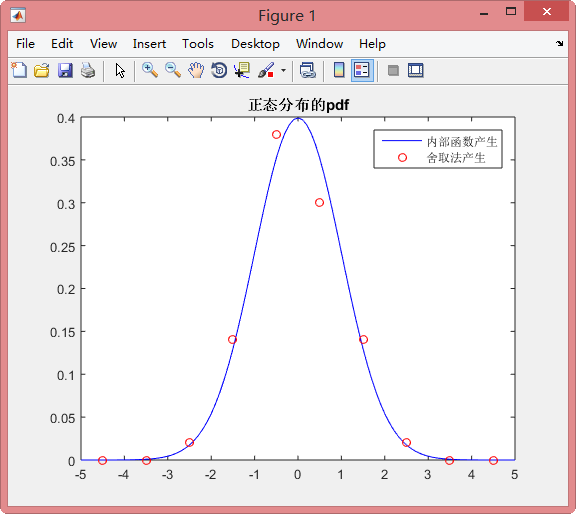
注意：使用这种方法的时候必须使$V$服从合适的分布来保证$M<+\infty$，如若找不到这样的分布，则可以参考Markov Chain Monte Carlo(MCMC)方法。

特殊方法

上述的两种通用方法基本上可以用均匀分布产生大多数连续分布，不过由于每种分布有着各自的特性，因此也可以通过特殊的方法来生成。下面以生成标准正态分布(正态分布性质表明：任何正态分布都可以由标准正态分布转化得到)为例：

中心极限定理法

中心极限定理是概率论中的一组定理。中心极限定理说明，大量相互独立的随机变量，其均值的分布以正态分布为极限。这组定理是数理统计学和误差分析的理论基础，指出了大量随机变量之和近似服从正态分布的条件。（摘自维基百科）
我们由中心极限定理可知，多个独立同分布的随机变量的和服从正态分布，而关于这个正态分布的均值和方差的确定，我们可以依据林德伯格－列维定理：
林德伯格－列维(Lindeberg-Levy)定理：
设随机变量$X1,X_2,\cdots,X_n$，且具有有限的数学期望$E({X_i}) = u,D( {X_i}) = {\sigma ^2} = 0\left( {i = 1,2, \cdots ,n} \right)$。记$\bar X = \frac{1}{n}\sum\limits{i = 1}^n {Xi} ,Y = \frac{\bar X - u}{\sigma /\sqrt n }$，则$\mathop {\lim }\limits{n \to \infty } P( Y < z ) = \Phi ( z )$，其中$\Phi( z)$是标准正态分布的分布函数。

在程序实现中，我利用$10$个相互独立的服从区间$-5$到$5$的均匀分布来生成标准正态分布$Y$。而由公式可知，区间$0$到$1$的均匀分布的均值为$u=\frac{ - 5 + 5}{2}=0,\sigma^2=(5-(-5))^2/12=100/12$.因此我们需要生成的服从标准正态的随机变量的表达式为：$Y = \frac{\bar X - 0.5}{\sqrt {100/12}/\sqrt n }$。具体程序实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
%-------------------正态分布-----------------------%
%参数：均值mu，方差sigma2
%mean=mu,  var=sigma2
clear all
close all
clc
mu=0;
sigma2=1;
n=10;%x的取值为正负无穷大，
%------------------由内置函数直接给出--------------%
%正态分布的产生X
X=normrnd(mu,sqrt(sigma2));%产生均值mu，方差sigma2的正态分布

%正态分布的cdf
x=0:.1:n;
Fx=normcdf(x,mu,sqrt(sigma2));
% figure
% plot(x,Fx,'-')
% title('正态分布的cdf')

%指数分布的pdf
x=-5:.1:5;
Px=normpdf(x,mu,sqrt(sigma2));
figure
plot(x,Px,'b-')
hold on
%-------------------由中心极限定理推导出---------------------%
N=1000;%样本点数
A=-5;%A,B位均匀分布的取值区间
B=5;

for i=1:10
U(i,1:N)=unifrnd(A,B,1,N);%U存储10个独立的服从均匀分布的随机变量
end
meanX=mean(U);
X2=(meanX-(A+B)/2)/sqrt((B-A)^2/12)*sqrt(10);%由林德伯格－列维定理的公式知X2服从正态分布
mean(X2);

%下面的程序是计算通过中心极限定理法生成的正态分布X2的pdf
Max=ceil(max(X2));
step=1;
range=A:step:B;

for i=1:length(range)-1
    YY(i)=sum(range(i)<=X2&X2<=range(i+1))/N/step;
    XX(i)=(range(i)+range(i+1))/2;
end

plot(XX,YY,'ro')
hold on
title('正态分布的pdf')
legend('内部函数产生','中心极限定理法产生')

显示结果如下：
图4

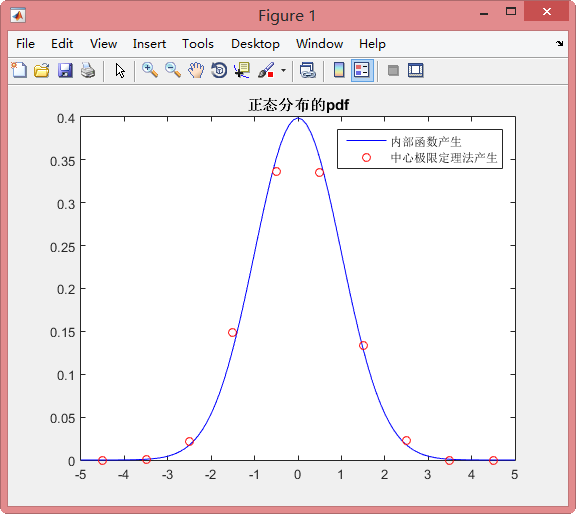
Box-Muller法

基本思想：假设$U,V$是两个相互独立的且服从区间在$0$到$1$的均匀分布，并且随机变量$X,Y$的表达式如下：

则$X,Y$是相互独立的，并且服从标准正态分布。

具体的程序实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
%-------------------正态分布-----------------------%
%参数：均值mu，方差sigma2
%mean=mu,  var=sigma2
clear all
close all
clc
mu=0;
sigma2=1;
n=10;%x的取值为正负无穷大，
%--------------------由内置函数直接给出----------------------%
%正态分布的产生X
X=normrnd(mu,sqrt(sigma2));%产生均值mu，方差sigma2的正态分布

%正态分布的cdf
x=0:.1:n;
Fx=normcdf(x,mu,sqrt(sigma2));
% figure
% plot(x,Fx,'-')
% title('正态分布的cdf')

%指数分布的pdf
x=-5:.1:5;
Px=normpdf(x,mu,sqrt(sigma2));
figure
plot(x,Px,'r-')
hold on

%-----------------------Box-Muller法-----------------------%
N=1000;
U=rand(1,N);%U,V都是服从(0,1)的均匀分布
V=rand(1,N);
A=-5;
B=5;
R=sqrt(-2.*log(U));
theta=2*pi*V;

X2=R.*cos(theta);
Y2=R.*sin(theta);%X，Y都是服从n(0,1)的正态分布

%下面的程序是计算通过Box-Muller法生成的正态分布X的pdf
Max=ceil(max(X2));
step=1;
range=A:step:B;

for i=1:length(range)-1
    YY(i)=sum(range(i)<=X2&X2<=range(i+1))/N/step;
    XX(i)=(range(i)+range(i+1))/2;
end

plot(XX,YY,'bo')
hold on
title('正态分布的pdf')
legend('内部函数产生','Box-Muller法产生')

显示结果如下：
图5

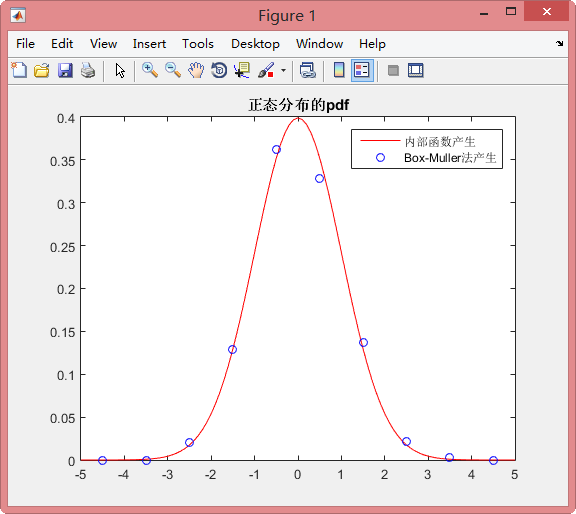
上面我们是以正态分布为例来讲述了特殊法的运用，主要是运用了正态分布与其他分布的关系：多个独立同分布的随机变量和服从正态分布；均匀分布与正态分布之间满足Box-Muller法中的关系。因此，当想要由一种分布生成另一种分布的时候，只需要知道它们之间的关系即可！

坚持原创技术分享，您的支持将鼓励我继续创作！