离过年都不到十天了,还要等到这周五才能回家,想想也一年没回家了。从寒假开始到现在,已经有二十来天,这期间把2014年总结中的寒假计划也大多数完成了:The Element Of Style的阅读,三门数学课《随机过程》、《工程优化》、《数值分析》的算法实现。回家过年期间肯定不会写博客了,今天一看,这个月只写了三篇,于是乎今天必须再写一篇来完成这个月的基本工作量。言归正传,这篇文章写写选修课《算法设计》作业题中的矩阵乘法的三种方法。
矩阵乘法
传统方法
- 理论公式
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void TraditionalMethod(float A[][N],float B[][N],float C[][N])//传统方法,三重循环
{
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
C[i][j]=0;//之所以每次调用都清零,是因为前面是循环调用,如果只调用一次就不需要
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
for(int k=0;k<N;k++)
{
C[i][j]=C[i][j]+A[i][k]*B[k][j];
}
}
}
}
分块相乘法
理论公式
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46void BlockMatrix()//分块矩阵计算
{
for(int i=0;i<N/2;i++)
for(int j=0;j<N/2;j++)
{
A11[i][j]=A[i][j];
A12[i][j]=A[i][j+N/2];
A21[i][j]=A[i+N/2][j];
A22[i][j]=A[i+N/2][j+N/2];
B11[i][j]=B[i][j];
B12[i][j]=B[i][j+N/2];
B21[i][j]=B[i+N/2][j];
B22[i][j]=B[i+N/2][j+N/2];
C11[i][j]=0;
C12[i][j]=0;
C21[i][j]=0;
C22[i][j]=0;
} //将矩阵A和B式分为四块
MATRIX_Multiply(N/2,A11,B11, AA);
MATRIX_Multiply(N/2,A12,B21, BB);
MATRIX_ADD(N/2,AA,BB,C11); //矩阵加法函数X+Y—>Z
MATRIX_Multiply(N/2,A11,B12, AA);
MATRIX_Multiply(N/2,A12,B22, BB);
MATRIX_ADD(N/2,AA,BB,C12); //矩阵加法函数X+Y—>Z
MATRIX_Multiply(N/2,A21,B11, AA);
MATRIX_Multiply(N/2,A22,B21, BB);
MATRIX_ADD(N/2,AA,BB,C21); //矩阵加法函数X+Y—>Z
MATRIX_Multiply(N/2,A21,B12, AA);
MATRIX_Multiply(N/2,A22,B22, BB);
MATRIX_ADD(N/2,AA,BB,C22); //矩阵加法函数X+Y—>Z
for(int i=0;i<N/2;i++)//将上面计算得到的结果放入结果矩阵C中
for(int j=0;j<N/2;j++)
{
C[i][j]=C11[i][j];
C[i][j+N/2]=C12[i][j];
C[i+N/2][j]=C21[i][j];
C[i+N/2][j+N/2]=C22[i][j];
} //计算结果送回C[N][N]
}
Strassen法
理论公式
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71void STRASSEN() //STRASSEN函数
{
int i,j;//,x;
for(i=0;i<N/2;i++)
for(j=0;j<N/2;j++)
{
A11[i][j]=A[i][j];
A12[i][j]=A[i][j+N/2];
A21[i][j]=A[i+N/2][j];
A22[i][j]=A[i+N/2][j+N/2];
B11[i][j]=B[i][j];
B12[i][j]=B[i][j+N/2];
B21[i][j]=B[i+N/2][j];
B22[i][j]=B[i+N/2][j+N/2];
} //将矩阵A和B式分为四块
MATRIX_SUB(N/2,B12,B22,BB);
MATRIX_Multiply(N/2,A11,BB,M1);
MATRIX_ADD(N/2,A11,A12,AA);
MATRIX_Multiply(N/2,AA,B22,M2);//M2=(A11+A12)B22
MATRIX_ADD(N/2,A21,A22,AA);
MATRIX_Multiply(N/2,AA,B11,M3);//M3=(A21+A22)B11
MATRIX_SUB(N/2,B21,B11,BB);
MATRIX_Multiply(N/2,A22,BB,M4);//M4=A22(B21-B11)
MATRIX_ADD(N/2,A11,A22,AA);
MATRIX_ADD(N/2,B11,B22,BB);
MATRIX_Multiply(N/2,AA,BB,M5);//M5=(A11+A22)(B11+B22)
MATRIX_SUB(N/2,A12,A22,AA);
MATRIX_ADD(N/2,B21,B22,BB);
MATRIX_Multiply(N/2,AA,BB,M6);//M6=(A12-A22)(B21+B22)
MATRIX_SUB(N/2,A11,A21,AA);
MATRIX_ADD(N/2,B11,B12,BB);
MATRIX_Multiply(N/2,AA,BB,M7);//M7=(A11-A21)(B11+B12)
//计算M1,M2,M3,M4,M5,M6,M7(递归部分)
MATRIX_ADD(N/2,M5,M4,MM1);
MATRIX_SUB(N/2,M2,M6,MM2);
MATRIX_SUB(N/2,MM1,MM2,C11);//C11=M5+M4-M2+M6
MATRIX_ADD(N/2,M1,M2,C12);//C12=M1+M2
MATRIX_ADD(N/2,M3,M4,C21);//C21=M3+M4
MATRIX_ADD(N/2,M5,M1,MM1);
MATRIX_ADD(N/2,M3,M7,MM2);
MATRIX_SUB(N/2,MM1,MM2,C22);//C22=M5+M1-M3-M7
for(i=0;i<N/2;i++)
for(j=0;j<N/2;j++)
{
C[i][j]=C11[i][j];
C[i][j+N/2]=C12[i][j];
C[i+N/2][j]=C21[i][j];
C[i+N/2][j+N/2]=C22[i][j];
} //计算结果送回C[N][N]
}
- 完整程序实现
1 | #include <iostream> |
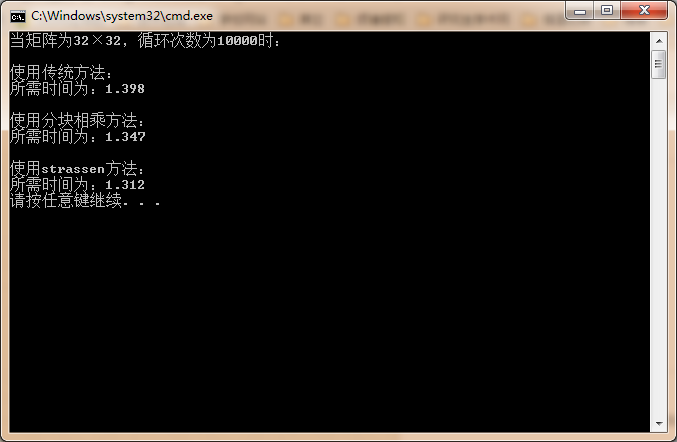
运行结果如下图: