牛顿法
使用条件:目标函数具有二阶导数,且海塞矩阵正定。
优缺点: 收敛速度快、计算量大、很依赖初始点的选择。
算法的基本步骤:
已知目标函数$f(x)$,梯度$g(x)$, Hessan矩阵$G(x)$, 给定误差限$\epsilon$:
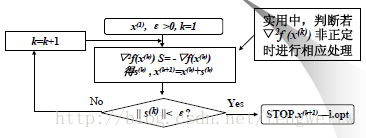
- 步骤1:选定初始点$x_0$,计算$f_0=f(x_0), k=0$;
- 步骤2:计算$g_k=g(x_k)$,如果$\Vert g_k\Vert\le\epsilon$, 算法停止, $x^\star=x_k$,否则转到步骤3:
- 步骤3:计算$G_k=G(x_k)$, 由方程$G_kd^k=-g_k$, 解得$d^k$;
- 步骤4:令$x_{k+1}=x_k+d^{k}, k=k+1$, 转到步骤2
算法流程图:
阻尼牛顿法
与牛顿法基本相同,只是加入了一维精确搜索。在牛顿迭代中,取$d^{(k)}=-[\nabla^2f(x^{(k)}) ]^{-1}\nabla f(x^{(k)}) $ , 加入精确一维搜索:$\min f(x^{(k)}+\lambda_kd^{(k)})$, 求得$\lambda_k$, 然后更新:$x^{(k+1)}=x^{(k)}+\lambda_kd^{(k)}$.
优缺点:改善了局部收敛性。
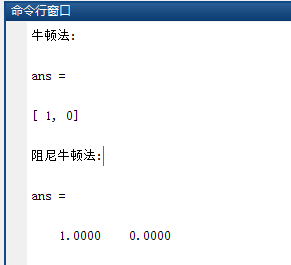
我们假设要求$f=(x-1)\cdot(x-1)+y\cdot y$的最小值,具体算法实现如下,只需要运行NTTest.m文件,其它函数文件放在同一目录下即可:
1、脚本文件NTTest.m
1 | clear all |
2、minNT.m
1 | function [x,minf]=minNT(f,x0,var,eps) |
3、minMNT.m
1 | function [x,minf]=minMNT(f,x0,var,eps) |
4、minHJ.m
1 | function [x,minf]=minHJ(f,a,b,eps) |
5、minJT.m
1 | function [minx,maxx]=minJT(f,x0,h0,eps) |
6、Funval.m
1 | function fv=Funval(f,varvec,varval) |
运行结果如下图:
单纯形法
单纯形法的理论还有点复杂,而本文主要针对算法的基本实现,因此,理论部分就此略过,详情可以参考网上的相关资料。下面给出具体的实现:
我们以具体实例来说明:
假定线性规划问题如下:
化为标准型可得:
具体的Matlab实现如下:
1、脚本文件:
1 | clear all |
2、ModifSimpleMthd.m文件
1 | function [x,minf]=ModifSimpleMthd(A,c,b,baseVector) |
运行结果如下图:

关于最优化的更多算法实现,请访问http://download.csdn.net/detail/tengweitw/8434549,里面有每个算法的索引说明,当然也包括上述算法。

