【工程优化】一维搜索方法

一维搜索方法的分类如下：

这篇文章主要讲解黄金分割法、二分法、牛顿法这三种一维搜索方法。黄金分割法只用到原函数，二分法用到函数的一阶导，牛顿法用到函数的二阶导。由于本文主要对研一上学期的课程中的部分算法进行程序实现，理论部分大多参考上课的课件。

---

黄金分割法

基本概念：

算法思想：

算法流程图及优缺点如下：

---

二分法

基本思想：

牛顿法

基本思想：

算法流程图：

具体实现：

下面我们通过程序具体实现，在程序中，我们设置原函数都是$f(x)=\sin(x)/x$，搜索区间都是$[0,1]$，牛顿法中假设初始值设为1,具体程序如下所示：

#include<stdio.h>
#include<math.h>
/********************函数的定义、一阶导、二阶导的模块 BEGIN*************************/
/*****************************\
输入：x为自变量
输出：x自变量对应的函数值
\*****************************/
double Function(double x)
{
    return (x-0.5)*(x-0.5);//这里填写函数式f(x),根据自己的函数修改
}
/*****************************\
输入：x为自变量
输出：x自变量对应的一阶导数值
\*****************************/
double Derivative(double x)//求函数的一阶导数
{
    double eps=0.0000001;//精度控制
    double dx=0.5;//设置初始的间隔，太大需要迭代多次，太小缺乏精度
    double dy=Function(x+dx)-Function(x);//函数值的增量
    double dd1=dy/dx;//导数
    double dd2=0;//dx变化时的导数
    dx=dx/2;//不断地减少x的增量
    dy=Function(x)-Function(x+dx);
    dd2=dy/dx;//计算新的导数值
    while(abs(dd1-dd2)>eps)//当相邻两次的导数值小于精度时终止迭代，得到导数
    {
        dd1=dd2;
        dx=dx/2.0;
        dy=Function(x+dx)-Function(x);
        dd2=dy/dx;
    }
    return dd2;
}
//求函数的2阶导数,与求一阶导数的原理一样，只需要把求函数值的函数Function换成求一阶导数的函数Derivative
/*****************************\
输入：x为自变量
输出：x自变量对应的二阶导数值
\*****************************/
double Derivative2(double x)
{
    double eps=0.00000001;
    double dx=0.5;
    double dy=Derivative(x+dx)-Derivative(x);
    double dd1=dy/dx;
    double dd2=0;
    dx=dx/2;
    dy=Derivative(x)-Derivative(x+dx);
    dd2=dy/dx;
    while(abs(dd1-dd2)>eps)
    {
        dd1=dd2;
        dx=dx/2.0;
        dy=Derivative(x+dx)-Derivative(x);
        dd2=dy/dx;
    }
    return dd2;
}
/********************函数的定义、一阶导、二阶导的模块  END*************************/
/******************************************\
输入：a，b为区间的上下限，n为最大的迭代次数
输出：打印函数最小值及对应的自变量x
\******************************************/
void GoldenSection(double a,double b,int n)//黄金分割法
{
    double l=a+0.382*(b-a);
    double h=a+0.618*(b-a);
    double region=b-a;
    
    double fl;
    double fh;
    int num=1;//迭代次数
    
    while(region>0.0000000001&&num<n)
    {
        fl=Function(l);
        fh=Function(h);
        if(fl>fh)
        {
            a=l;
            l=h;
            h=a+0.618*(b-a);
        }
        else
        {
            b=h;
            h=l;
            l=a+0.382*(b-a);
        }
        num++;
        region=abs(b-a);
    }
    if(num==n)
        printf("找不到最小值");
    else
    {
        printf("黄金分割法:x=%f时，最小值f(x)=%f",(a+b)/2,Function((a+b)/2));
        
    }
}
/******************************************\
输入：a，b为区间的上下限
输出：打印函数最小值及对应的自变量x
\******************************************/
void Dichotomy(double a,double b)//二分法
{
    double eps=0.0000001;
    double x=(a+b)/2;
    double region=b-a;
    double fxDerivative= Derivative(x);
    while(region>0.0000001&&abs(fxDerivative)>eps)
    {
        fxDerivative= Derivative(x);
        if(fxDerivative>eps)
            b=x;
        if(fxDerivative<-eps)
            a=x;
        x=(a+b)/2;
        region=abs(b-a);
    }
    printf("\n\n二分法：x=%f时，f(x)=%f\n",x,Function(x));
}
/******************************************\
输入：a，b为区间的上下限，x1是初始值
输出：打印函数最小值及对应的自变量x
\******************************************/
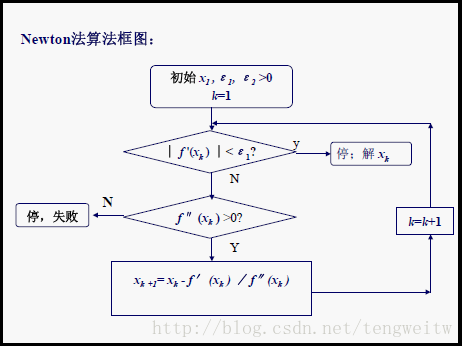
void Newton(double a,double b,double x1)
{
    double eps=0.0000001;
    double x=x1;
    double d1=Derivative(x1);//一阶导
    double d2;//二阶导
    while(abs(d1)>eps)
    {
        d2=Derivative2(x);
        if(d2<0)
            printf("二阶导小于0，无法求解");
        else
        {
            x=x-d1/d2;//x迭代公式
            d1=Derivative(x);
        }
    }
    printf("\n牛顿法：x=%f时，f(x)=%f\n\n",x,Function(x));
}
void main()
{
    GoldenSection(0,1,100000);//黄金分割法
    
    Dichotomy(0,1);//二分法
    Newton(0,1,1);//牛顿法
}

运行结果如下图：