【数值分析】误差的分析与减少及Matlab解线性方程的四种方法

误差的来源

• 模型误差：数学模型与实际问题之间的误差
• 观测误差：测量数据与实际数据的误差
• 方法误差：数学模型的精确解与数值方法得到的数值解之间的误差：例如
• 舍入误差：对数据进行四舍五入后产生的误差

---

减少误差的几种方法

​ 现在，我们一般用计算机解决计算问题，使用最多的是Matlab软件。对实际问题进行数学建模时，可能存在模型误差，对数学模型进行数值求解时，我们使用的方法可能产生方法误差，我们输入计算机的数据一般是有测量误差的，计算机在运算过程的每一步又会产生舍入误差（十进制转化为二进制时可能产生舍入误差）。由此看来，解决一个问题，基本上会有以上四种四种误差。记得高中物理老师说过，错误是可以避免的，误差是不可避免的，我们只可以减少误差。下面我们就来介绍减少误差的几种方法：

• 避免两个相近的数相减
  比如: 当$x=10003$时，计算$\sqrt{x+1}-\sqrt{x}$的近似值。
  如果使用$6$位十进制浮点运算，运算时取$6$位有效数字，结果如下：

  $$\sqrt{x+1}-\sqrt{x}=100.020-100.015=0.005$$

  结果只有一位有效数字，与之前相比，损失了$5$位有效数字。

  如果使用下面的方法：

  $$\sqrt{x+1}-\sqrt{x}=\frac{1}{\sqrt{x+1}+\sqrt{x}}=\frac{1}{100.020+100.015}=0.00499913$$

  则结果有$6$位有效数字，与精确值$0.00499912523117984\cdots$较为接近。

• 防止重要的小数被大数吃掉
  比如: 已知$x=3\times 10^{12},y=7,z=-3\times 10^{12}$,求$x+y+z$
  如果按照$(x+y)+z$的顺序来求的话，由于$x$远大于$y$，在计算机中可能导致$x+y=x$的情况，因此我们可以按照$(x+z)+y$的顺序计算得到正确的结果。

• 避免除数的绝对值远小于被除数的绝对值
  比如：用消去法解线性方程组

  $$\left\{\begin{array}{l} 0.00003x_1-3x_2=0.6\\x_1+2x_2=1\end{array}\right.$$

  这个方程组的正确解为：

  $$x_1=1.399972, x_2=-0.199986$$

  对于上述方程组，当我们将第一个方程除以$0.00003$减去第二个方程时，可以得到下面的化简和计算结果：

  $$\left\{\begin{array}{l} 0.00003x_1-3x_2=0.6\\-100000x_2=20000\end{array}\right.\rightarrow \left\{\begin{array}{l} x_1=0\\x_2=-0.2\end{array}\right.$$

  显然上述结果严重失真，产生了很大的误差。这就是由于除数的绝对值远小于被除数的绝对值造成的。为了避免上述情况，我们可以用第二个方程消去第一个方程中的$x_1$，即第二个方程乘以$0.00003$减去第一个方程，得到如下表达式和结果：

  $$\left\{\begin{array}{l}-3x_2=0.6\\x_1+2x_2=1\end{array}\right.\rightarrow \left\{\begin{array}{l} x_1=1.4\\x_2=-0.2\end{array}\right.$$

  将结果与正确解相比发现，这是一组相当好的近似解。

• 注意算法的稳定性
  所谓算法的稳定性是指，一个算法如果输入数据有误差，而在计算过程中误差不增长，那么称此算法是数值稳定的。

---

上面的部分基本上都来源于《数值分析》一书，讲的挺好的，这些减小误差的方法，我们平时需要多注意，在用c进行编程实现时需要注意，而用Matlab实现时，上面的问题都不是问题了，不过我们要学习的是这种方法和技巧。下面讲讲，在实现上述方法的Matlab的知识：1、精度控制；2、解线性方程组。

精度控制

• format digits vpa函数的使用
• format只用来控制显示精度的，并不控制计算精度，digits用来控制计算精度，vpa也是控制计算精度。
• digits必须与vpa配合使用，单独不起作用。

• vpa可单独控制计算精度

  具体操作如下图：

1. ​ format的操作

   

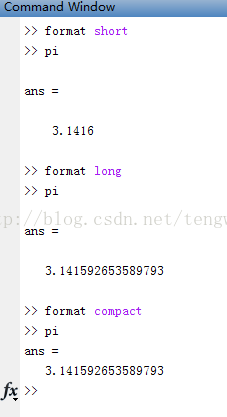
2. ​ digits的操作
   

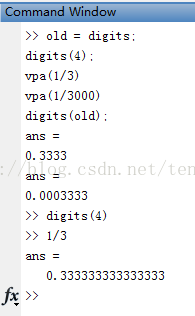
3. ​ vpa的操作
   

---

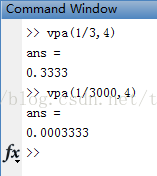
解非齐次线性方程组

$$\left\{\begin{array}{l} 6x_1+2x_2+3x_3+4x_4+5x_5=80\\ 2x_1-3x_2+7x_3+10x_4+13x_5=59\\ 3x_1+5x_2+11x_3-16x_4+21x_5=90\\ 2x_1-7x_2+7x_3+7x_4+2x_5=22\\ 7x_1+3x_2-5x_3+3x_4+10x_5=85 \end{array}\right.$$

可以通过以下四种方法求解该方程组：

用矩阵表示上述的线性方程组如下：

$$A=\left[\begin{array}{ccccc}6&2&3&4&5\\2&-3&7&10&13\\3&5&11&-16&21\\2&-7&7&7&2\\7&3&-5&3&10\end{array}\right], b=\left[\begin{array}{c}80\\59\\90\\22\\85\end{array}\right]$$

• 求逆矩阵法

  $$Ax=b\rightarrow x=A^{-1}b$$

• 矩阵左除法

  $$x=A\backslash b$$

• 初等行变换

  $$Ax=b\rightarrow x=A^{-1}b\rightarrow rref\left[\begin{array}{c}A&b\end{array}\right]=\left[\begin{array}{c}A^{-1}A&A^{-1}b\end{array}\right]=\left[\begin{array}{c}I&x\end{array}\right]$$

• 卡莱姆法则

  $$x_i=\frac{\det(A_i)}{\det(A)}$$

具体的程序实现如下：

clear all
clc
 
A=[ 6 2 3 4 5
    2 -3 7 10 13
    3 5 11 -16 21
    2 -7 7 7 2
    7 3 -5 3 10]
b=[80 59 90 22 85]'
 
x1=inv(A)*b%逆矩阵法
x2=A\b%矩阵左除法
x3=rref([A b])%初等行变换
 
%克拉姆法则
for i=1:length(A)
    B=A;
    B(:,i)=b;
    x(i)=det(B)/det(A);
end
x'

运行结果如下图：

注意事项：当系数矩阵$A$不是方阵，或$A$的行列式为$0$时，逆矩阵法和克拉姆法则无法使用，而初等行变换能适用于各种线性方程组的求解。