【线性代数】正交投影

​ 我们在初中就应该学过投影，那么什么是投影呢？形象点说，就是将你需要投影的东西上的每一点向你要投影的平面作垂线，垂线与平面的交点的集合就是你的投影。注意这里我们的投影是向量的投影，几何的投影(并不一定是垂直投影的)可见度娘百科。同样的，我们从简单的二维投影来开始讨论。

---

二维投影

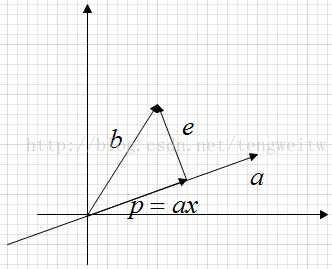
上图表示的是，向量$b$在向量$a$上的投影为$p$。显然有如下表达式：

$$e=b-p=b-xa\\ a^Te=0\rightarrow a^T(b-xa)=0\rightarrow xa^Ta=a^Tb\rightarrow x=\frac{a^Tb}{a^Ta}\\ p=ax=a\frac{a^Tb}{a^Ta}\\ Pb=p\rightarrow P=\frac{aa^T}{a^Ta}$$

其中，$P$为投影矩阵，由$P$的表达式可以看出，它具有如下性质：

$$P^T=P, P^2=P$$

---

三维投影

三维投影，就是将一个向量投影到一个平面上。同上面一样，假设$b$向量在平面上的投影为$p$，则有表达式：

$$e=b-p$$

$e$是垂直于平面的向量。由于$p$向量在平面上，则$p$向量可以由该平面的$2$个线性无关向量(正如，在$xy$平面的任何向量都可以由$x$轴，$y$轴表示)表示：

$$p=x_1a_1+x_2a_2=Ax\\ A=[a_1\quad a_2]\\ x=[x_1\quad x_2]^T$$

由于$e$垂直于平面，则$e$向量垂直于平面中的任意向量，则有：

$$\begin{aligned} \left\{ \begin{array}{**lr**} e=b-p=b-Ax\\ a_1^T(b-Ax)=0\\ a_2^T(b-Ax)=0 \end{array} \right. \rightarrow \left[\begin{array}{c}a_1^T\\a_2^T\end{array}\right]\left[b-Ax\right]=0\rightarrow A^T(b-Ax)=0 \end{aligned}$$

将上式化简求得$x$：

$$A^TAx=A^Tb\rightarrow x=(A^TA)^{-1}A^Tb$$

又因为$p=Ax$, $Pb=p$，则得到投影矩阵为：

$$P=A(A^TA)^{-1}A^T$$

由$P$的表达式可以看出，它具有如下性质：

$$P^T=P, P^2=P$$

上面的投影矩阵是通式，当投影在一维情况时，$A$即为直线上的任意一个向量$a$,投影矩阵为：

$$P=A(A^TA)^{-1}A^T=a(a^Ta)^{-1}a^T=\frac{aa^T}{a^Ta}$$

注意：一个数值的逆是它的倒数。

---

举例说明

下面以一个实例来说明：

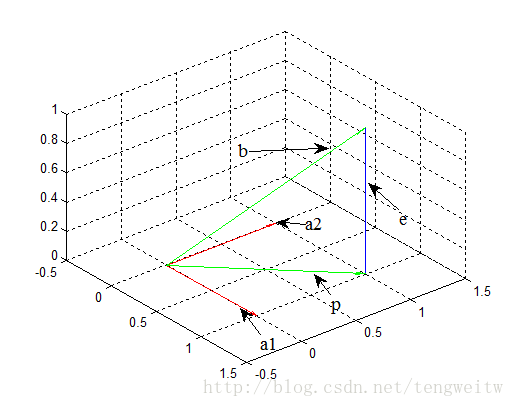
如上图，假设我们要将向量$b$投影到水平面上，其投影为$p$，$a_1$, $a_2$为水平面的两个线性无关向量，它们的参数分别为：

$$b=\left[\begin{array}{c}1\\1\\1\end{array}\right], a_1=\left[\begin{array}{c}1\\0\\0\end{array}\right], a_2=\left[\begin{array}{c}0\\1\\0\end{array}\right]$$

那么$A=[a_1\quad a_2]$即：

$$A=\left[\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right]$$

由上面我们求得的通式，可得投影矩阵$P$:

$$P=A(A^TA)^{-1}A^T=\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right]$$

知道投影矩阵$P$后，我们可以得到$b$在水平面上的投影$p$为：

$$p=Pb=\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&0\end{array}\right] \left[\begin{array}{c}1\\1\\1\end{array}\right]=\left[\begin{array}{c}1\\1\\0\end{array}\right]$$

显然，$p$与我们图中所示的结果相同。这里我们是以三维情况进行举例的，更高维情况，我们无法用图像来描述，但是通式也是成立的。

三维图的matlab程序如下：

clear all
clc
 
a1=[1 0 0];
a2=[0 1 0];
b=[1 1 1];
p=[1 1 0];
e=b-p;
quiver3(0,0,0,a1(1),a1(2),a1(3),1,'color','r')
hold on
quiver3(0,0,0,a2(1),a2(2),a2(3),1,'color','r')
hold on
quiver3(0,0,0,b(1),b(2),b(3),1,'color','g')
hold on
quiver3(0,0,0,p(1),p(2),p(3),1,'color','g')
hold on
quiver3(p(1),p(2),p(3),e(1),e(2),e(3),1,'color','b')