【线性代数】正交向量与正交子空间

在前面文章《矩阵的四个基本子空间》中提到：

​ 一个秩为$r$，$m\times n$的矩阵$A$中，其行空间和列空间的维数为$r$，零空间和左零空间的维数分别为$n-r$，$m-r$，并且有行空间与零空间正交，列空间与左零空间正交。

​ “掌握上面的这个结论就掌握了线性代数的半壁江山！”，MIT教授如是说。那么什么是正交子空间呢？我们首先从我们熟悉的正交向量说起。

---

正交向量

我们都知道，如果两个向量$x,y$正交，则其夹角为$90$度，可表示为表达式：

$$x^Ty=0$$

注意：$x, y$的顺序没有区别，即下式也成立：

$$y^Tx=0$$

两个向量正交，可以表示为下图：

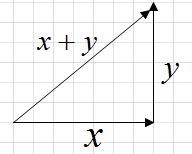
由勾股定理可知：

$$\Vert x\Vert^2+\Vert y\Vert^2=\Vert x+y\Vert^2$$

将上式展开得：

$$x^Tx+y^Ty=(x+y)^T(x+y)=x^Tx+y^Ty+x^Ty+y^Tx\\ 0=x^Ty+y^Tx\rightarrow x^Ty=y^Tx=0$$

我们举例说明：假设两个向量分别为$x, y, z=x+y$：

$$x=\left[\begin{array}{c}1\\2\\3\end{array}\right], y=\left[\begin{array}{c}2\\-1\\0\end{array}\right], z=x+y=\left[\begin{array}{c}3\\1\\3\end{array}\right],$$

其中$x, y$满足下式：

$$x^Ty=y^Tx=0$$

则向量的长度（即向量的$2$范数）的平方为：

$$\Vert x\Vert^2=14, \Vert y\Vert^2=5,\Vert z\Vert^2=19$$

显然满足勾股定理. 上面的推导，已证明勾股定理，自己可以仔细领会。

---

正交子空间

定义：两个子空间正交即两个子空间的任意两个向量正交。

文章开头说到，行空间与零空间正交，列空间与左零空间正交。下面我们来证明行空间与零空间正交，列空间与左零空间正交。

行空间与零空间正交的证明

在《矩阵的零空间》一文中，我们知道，$Ax=0$的解就是矩阵的零空间，则：

$$Ax=0\rightarrow x=\left[\begin{array}{c}row_1\\row_2\\\vdots\\row_3\end{array}\right]x=0$$

展开可得：

$$\begin{aligned} \left\{ \begin{array}{**lr**} row_1^Tx=0 \\ row_2^Tx=0 \\ row_3^Tx=0 \end{array} \right. \rightarrow \begin{array}{**lr**} row_1^Tx+row_2^Tx+\cdots+row_n^T=0 \end{array} \end{aligned}$$

上式说明，矩阵的每一行向量都与零空间正交，而矩阵的行空间就是其行向量的线性组合，则说明行空间与零空间正交。同理，我们亦可以证明列空间与左零空间正交，在此就不重复了。