前面的关于线性代数的文章都是从数学的角度来讲解的,本文将换个角度来讲解问题。导师时常告诉我,凡事都要想想它的物理或实际意义,需要透过现象看本质,这样就能更加深刻的理解,这样就可以看看线性代数有什么实际的用途。
假设有如下电路网络:
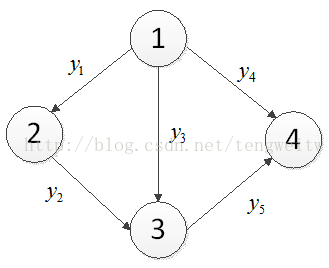
图中有$1, 2, 3, 4$号节点,$y_1, y_2, y_3, y_4, y_5$五条边,箭头的指向标明可以电流流向。我们假设电流的出发点设为$-1$,到达点设为$1$,则我们可以通过矩阵来表示上述网络:
矩阵零空间的物理意义
我们首先考虑矩阵$A$的零空间,则有:
从上面的式子可以看出$Ax$的结果是各个节点之间的差值,假设$x_i$为第$i$点的电势,那我们就赋予了物理意义:$Ax=0$的意思是当节点电势取何值时,所有的节点之间的电势差为$0$。很显然,当所有节点等电势时显然成立,即:
我们将图中各边的电流用$b$表示,则有等式$Ax=b$。其中$A$表示了电路节点之间的关系,$x$代表了各点的电势,$b$代表了各边的电流。这样,我们就将一个物理问题数学化了。上面讨论中$b=0$,$x$中各个分量相同,即说明电势相同,网络中没有电流,这与我们的物理常识是一致的:电势差是产生电流的原因。
矩阵左零空间的物理意义
上面我们看了矩阵$A$的零空间,下面我们讨论矩阵$A$的左零空间,为了给我们的式子赋予实际意义,在下式中,我们假设$y$为每条边的电流,$b$为每个节点的电流值,$b=0$说明电流为$0$。
该式反应的是电流中的基尔霍夫电流定律:流入一个节点的电流与流出的是相等的,即合电流为$0$:
举例说明,$-y_1-y_3-y_4=0$说明的是$1$号节点满足KCL的条件。我们可以通过高斯消元法求得解,但是我们可以通过图来得到解:
在电路网络图中,我们可以看到,$1, 2, 3$号节点构成一个回路,$1, 3, 4$号也构成一个回路,为了满足基尔霍夫电流定律,我们可以只让电流在回路中循环流动,即:我们可以得到两个特解:
那么左零空间可以表示为上述两个特解的线性组合。
对$A^T$进行消元,我们可以发现其秩是$3$,即列中有三行是线性无关的。由上面的两个特解,我们知道第$1, 2, 3$列是相关的,第$3, 4, 5$列是相关的,除此之外的任意三列都是线性无关的。我们发现$y_1, y_2, y_3$恰好构成回路,$y_3, y_4, y_5$也恰好构成回路,这说明相关性是由回路产生的。
欧拉公式的证明
欧拉公式:回路数=边数-顶点数+1
前面文章说过,如果一个$m\times n$的矩阵$A$的秩为$r$,则其左零空间的维数为$m-r$。在这里,左零空间的维数代表的是不相关的回路数,$m$代表的是边数,由于矩阵$A$的零空间是$1$维的,则列空间的维数为$r=n-1$。所以有下式成立(即欧拉公式):
不相关的回路数=边数-顶点数+1

