【算法导论】多项式求和

一般情况下，一元$n$次多项式可写成：

$$P_n(x)=p_1x^{e_1}+p_2x^{e_2}+\cdots+p_mx^{e_m}$$

其中，$p_i$是指数为$e_i$的项的非零系数，且满足

$$0\le e_1\le e_2\le\cdots\le e_m=n$$

因此，我们可以采用线性表（定义：线性表是由$n$个数据元素构成的有限序列，比如数组、向量、链表等等）来表示：

$$P=(p_0,p_1,\cdots,p_n)$$

其中，每一项的指数$i$可以用其系数$p_i$的序号表示。

---

在通常的应用中，多项式的次数比较大，使得线性表的长度很难确定，因此我们可以考虑链表，向量也可以（c++中）。举例说明：假如我们用数组来表示下面的多项式：

$$S_4(x)=5x^{1548}-19x^{123}+2x^2+1$$

​ 可见，我们需要一个大小为$1549$的数组来表示，而实际有用的信息只有数组中的$4$个元素，其他地方都是$0$，所以造成了空间浪费。并且如果我们事先不知道多项式的最高次项的指数，则我们需要定义一个足够大的数组来存储，这样做显然浪费了很多内存空间。我们可以使用链表来解决上述问题：

在计算机内，我们用一个结点来存放多项式的一项，为了节约空间，并和书写习惯一致，只需保留非零系数的项。每个结点分系数、指数和指针三个域，如下图所示，其中的指针next指明下一项的位置:

例如，下面多项式分别为$A,B$:

$$A_4(x)=7+3x+9x^8+5x^{17}\\ B_3(x)=8x+22x^7-9x^8$$

用循环链表可以表示如下：

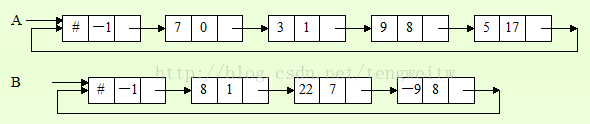
​ 两个多项式相加的运算规则很简单，对所有指数相同的项，将其对应系数相加，若和不为零，则构成和多项式中的一项；将所有指数不相同的项复制到和多项式中。具体实现时，我们以上面的多项式$A$，$B$为测试样例。可采用另建链表来存储和的多项式的方法，或采用把一个多项式归并入另一个多项式的方法。我们以后种方法为例,即将$A+B$的和多项式存储到$A$中。具体程序实现如下（我采用了循环链表）：

#include<stdio.h>
#include<stdlib.h>
#include<conio.h>

typedef struct pnode//用链表来存储多项式信息
{
	float coef;//多项式系数
	int   exp;//多项式指数
	struct pnode *next;
}polynode;

polynode *Create()
{
	float coef;
	int exp;
	polynode *head,*s,*r;
	head=(polynode*)malloc(sizeof(polynode));
	head->coef=0;
	head->exp=-1;
	r=head;
	printf("请输入各项的系数和指数：\n");
	while(1)
	{
		scanf("%f %d",&coef,&exp);
		if(coef!=0)//输入0 0来结束输入
		{
			s=(polynode*)malloc(sizeof(polynode));
			s->coef=coef;//s用来保存当前节点
			s->exp=exp;
			r->next=s;
			r=s;
		}
		else
			break;
	}

	r->next=head;//构造循环链表
	return head;

}

polynode*PolyAdd(polynode* pa,polynode* pb)//进行多项式相加
{
	polynode *p,*q,*r,*s;
	float x;
	p=pa->next;//分别指向多项式的第一项
	q=pb->next;
	s=pa;//s用于保存当前节点

	while((p!=pa)&&(q!=pb))//没有结束，回到链表头
	{
		if(p->exp<q->exp)//p的指数小于q的指数，将p放入链表中
		{
			s=p;
			p=p->next;
		}
		else if(p->exp>q->exp)//p的指数大于q的指数，将q放入链表中
		{
			r=q->next;
			q->next=p;
			s->next=q;
			s=q;
			q=r;
		}
		else//当两者指数相同时，进行合并
		{
			x=p->coef+q->coef;
			if(x!=0)
			{
				p->coef=x;
				s=p;
			}
			else//若合并结果为0，将该节点移除
			{
				s->next=p->next;
				free(p);
			}
					p=s->next;
		r=q;
		q=q->next;
		free(r);
		}

	}

	if(q!=pb)//如果多项式b的项数少于多项式a的情况
	{
		r=q;
		while(r->next!=pb)
			r=r->next;
		s->next=q;
		r->next=pa;
	}
	return pa;
}

void Output(polynode *head)// 输出多项式信息
{
	polynode *p;
	printf("系数和指数分别为：");
	p=head->next;
	while(p!=head)
	{
		printf("%.1f , %d    ",p->coef,p->exp);
		p=p->next;
	}
	printf("\n");
}

void main()
{
	polynode* ha,*hb;
	printf("\n建立多项式A:");
	ha=Create();
	Output(ha);
	printf("\n建立多项式B:");
	hb=Create();
	Output(hb);

	ha=PolyAdd(ha,hb);
	printf("\n多项式A+B：");
    Output(ha);
}

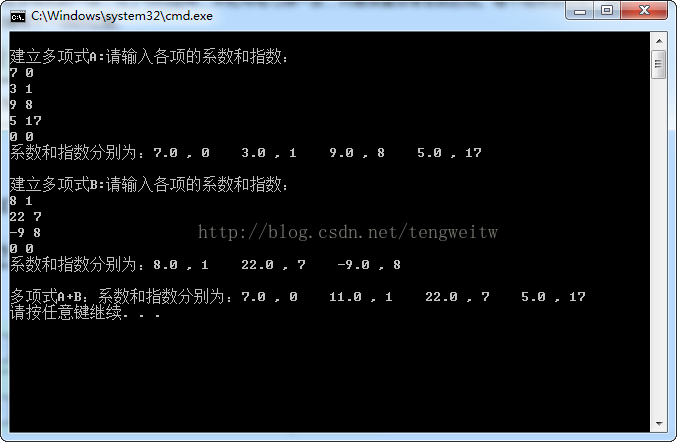
运行结果如下：