【线性代数】方程组的几何解释

二维情况

首先，给出如下的二元一次方程组：

$$\begin{aligned} 2x-y=0\\ -x+2y=3 \end{aligned}$$

我们初中就对上面的二元一次方程组进行过求解，求解很简单。但是我们现在利用线性代数来表示这个式子，上式可以表示为：

$$\begin{aligned} \underbrace{\left[ \begin{array}{cc} 2 & -1 \\ -1 & 2 \\ \end{array} \right ]}_{A}\underbrace{\left[\begin{array}{c}x\\y\end{array}\right]}_{\hat x} =\underbrace{\left[\begin{array}{c}0\\3\end{array}\right]}_{b} \end{aligned}$$

我们这里假设用小写字母表示向量，大写字母表示矩阵。上面可以二元一次方程组便转化为求解$x$,$y$。

下面我们从几种不同的角度来求解上面的方程组：

1、从行的角度看，也就是画出上面两个方程的图像：

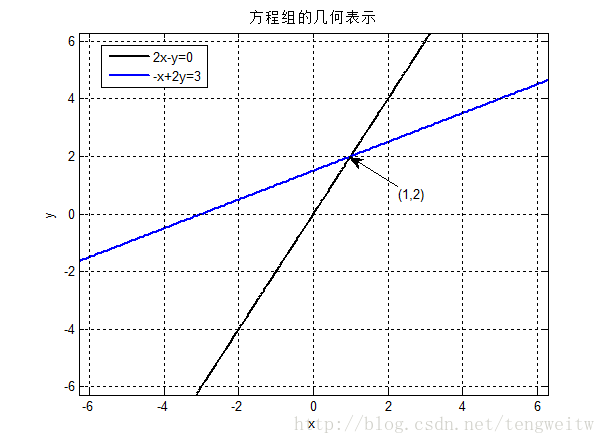
很明显的可以看出方程的解是$x=1, y=2$。

2、从列的角度看，方程组可以表现为列的线性组合：

$$\begin{aligned} x\left[\begin{array}{c}2\\-1\end{array}\right]+y\left[\begin{array}{c}-1\\2\end{array}\right]=\left[\begin{array}{c}0\\3\end{array}\right] \end{aligned}$$

令向量$a=[2,-1]’, b=[-1, 2]’, c=[0, 3]’$，则问题变为找到适当的$x,y$将向量$a, b$ 进行线性组合得到向量$c$。同样我们可以通过作图求解：

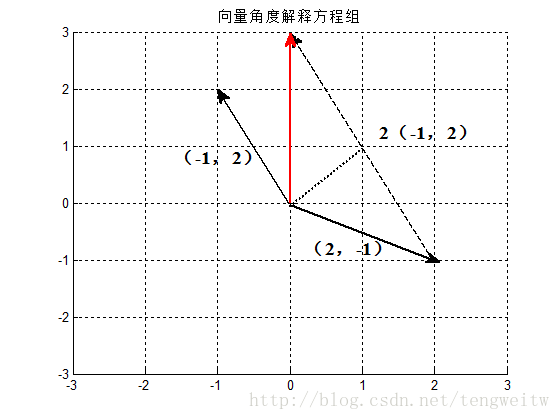
从上图可以看到$(2,-1)+2(-1,2)=(0,3)$，从而得到$x=1,y=2$。

---

三维情况

上面的问题都是在二维平面上进行求解的，下面来看看三维下的情况：首先，给出三元一次方程组：

$$\begin{aligned} 2x-y+0z&=0\\ -x+2y-z&=-1\\ 0x-3y+4z&=4 \end{aligned}$$

同样可以得到其矩阵的表示形式：

$$\begin{aligned} \left[\begin{array}{ccc}2&-1&0\\-1&2&-1\\0&-3&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\-1\\4\end{array}\right] \end{aligned}$$

还是按照上面的方法分析：

---

1、从行的角度看，也就是画出上面三个方程的图像（在这里变成了三维空间的平面）：

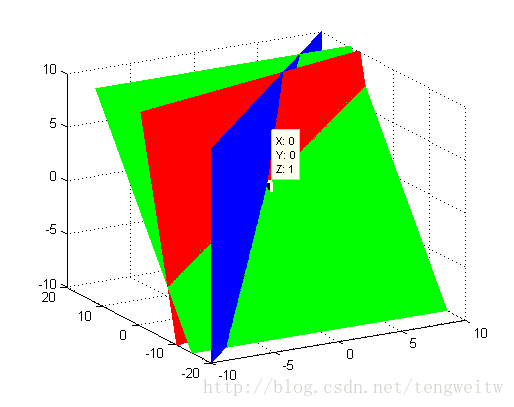
上图的matlab代码为：

figure
t=-10:.1:10;
[x,z]=meshgrid(t);
y=2*x;
mesh(x,y,z);
hold on
y=(x+z-1)/2;
mesh(x,y,z)
hold on
y=-(4-4*z)/3;
mesh(x,y,z)

然后人工进行一些修正即可。从图中可以看出，三个平面交于一点$(0, 0, 1)$也就是方程组的解：$x=0, y=0, z=1$。

---

2、同样从列的角度考虑该问题：

$$\begin{aligned} x\left[\begin{array}{c}2\\-1\\0\end{array}\right]+y\left[\begin{array}{c}-1\\2\\3\end{array}\right]+z\left[\begin{array}{c}0\\-1\\4\end{array}\right]=\left[\begin{array}{c}0\\-1\\4\end{array}\right] \end{aligned}$$

不用通过计算或作图，我们从上式就可以轻易得到$x=y=0,z=1$，这比上面一种方法要简单得多。

画出上面四个列向量的图（其中后两个列向量相同$(0,-1, 4)’$）:

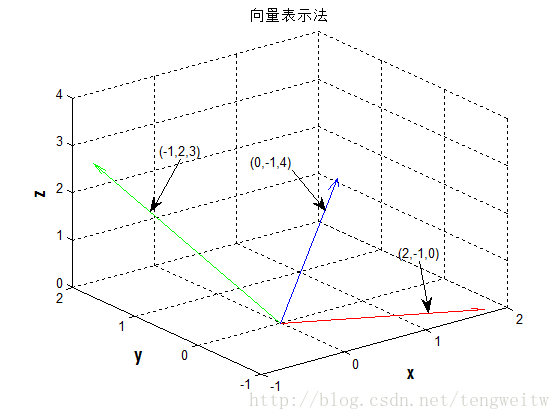
上图的matlab代码为：

a=[2 -1 0];
b=[-1 2 3];
c=[0 -1 4];
quiver3(0,0,0,a(1),a(2),a(3),'color','r')
hold on
quiver3(0,0,0,b(1),b(2),b(3),'color','g')
hold on
quiver3(0,0,0,c(1),c(2),c(3),'color','b')

然后人工标上箭头，当然也可以通过命令标上箭头。