说起幻方,大家应该在小学时候就已经接触过了,最简单的就是九宫格,射雕英雄传中的那段至今还记得:戴九履一,左三右七,二四为肩,六八为足。下面我们就来看看这个有趣的问题。
幻方可以分为:奇数阶幻方、双偶阶幻方、单偶阶幻方。
奇数阶幻方
上面所说的九宫格就是典型的奇数阶幻方,奇数阶幻方值得是阶数为奇数的幻方。其最经典的填法是罗伯法。首先 把$1$(或最小的数)放在第一行正中;按以下规律排列剩下的$(n^2-1)$个数,具体步骤为:
(1)每一个数放在前一个数的右上一格;
(2)如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;
(3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;
(4)如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在底行且最左列;
(5)如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
上述步骤可以总结为七言绝句:
先填上行正中央, 依次斜填切莫忘。 上格没有顶格填, 顶格没有底格放。—奇幻七绝
下面有人通过作图可以很好的解释这几句话,现借鉴如下:
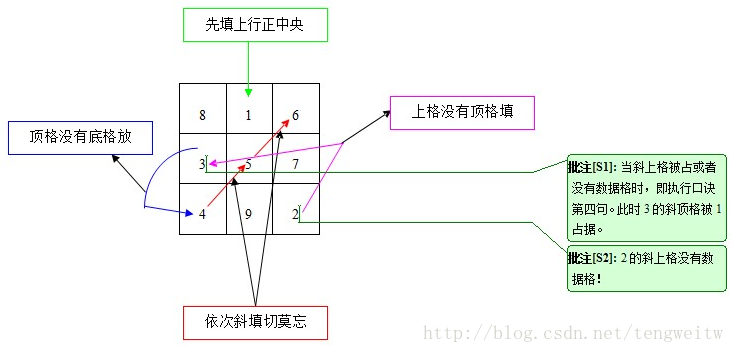
从上面的图可以看出,该图与我们前面的九宫格口诀不相符,上下颠倒了。但是这都是对的,本质上没有区别。
双偶数阶幻方
所谓双偶阶幻方就是当$n$可以被$4$整除时的偶阶幻方,即$4K$阶幻方。其最经典的填法为海尔法,下面以$8$阶幻方为例,具体的填法为:
(1)先把数字按顺序填。然后,按$4\times 4$把它分割成$4$块(如图)
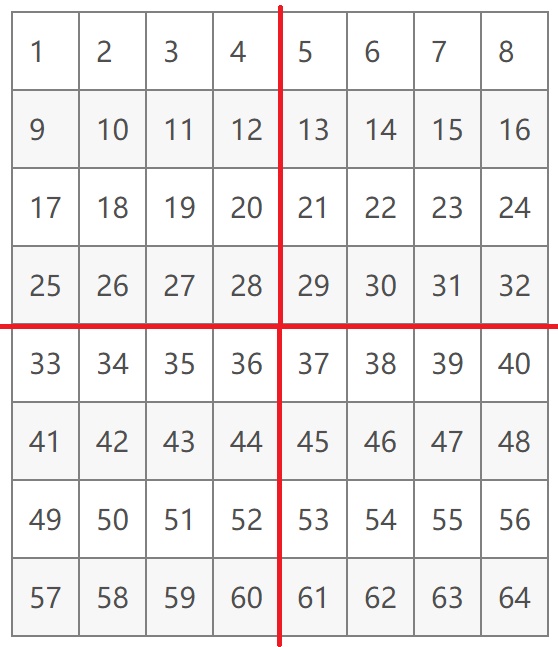
(2)每个小方阵对角线上的数字(如左上角小方阵部分),换成和它互补的数。
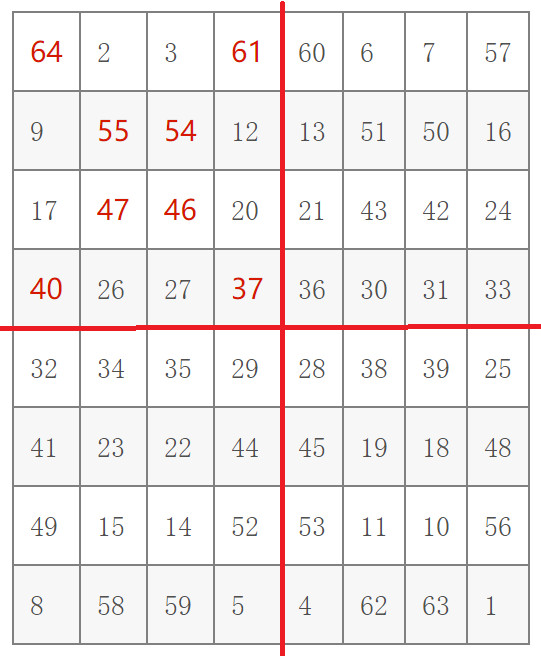
单偶数阶幻方
所谓单偶阶幻方就是当$n$不可以被$4$整除时的偶阶幻方,即$4K+2$阶幻方。如$(n=6, 10,\cdots)$的幻方。其经典的填法为斯特拉兹法,以$10$阶幻方为例,具体的步骤如下:
1)把魔方阵分为$A,B,C,D$四个象限,这样每一个象限肯定是奇数阶。用罗伯法,依次在$A$象限,$D$象限,$B$象限,$C$象限按奇数阶幻方的填法填数。
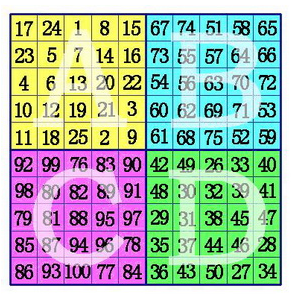
(2)在$A$象限的中间行、中间格开始,按自左向右的方向,标出$k$格。$A$象限的其它行则标出最左边的$k$格。将这些格,和$C$象限相对位置上的数互换位置。
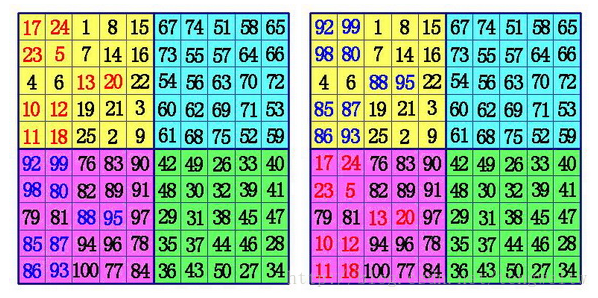
(3)在$B$象限所有行的中间格,自右向左,标出$k-1$格。(注:$6$阶幻方由于$k-1=0$,所以不用再作$B$、$D$象限的数据交换),将这些格,和$D$象限相对位置上的数互换位置。
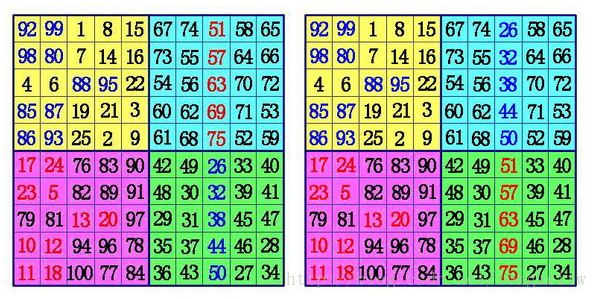
具体的程序实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
| #include<stdio.h>
bool check(int matrix[10][10],int n)
{
int sum=0;
int temp=0;
int i=0,j=0,k=0;
for( i=0;i<n;i++)
sum=sum+matrix[0][i];
for(j=1;j<n;j++)
{
temp=0;
for(k=0;k<n;k++)
temp=temp+matrix[j][k];
if(temp!=sum)
return false;
}
for( j=0;j<n;j++)
{
temp=0;
for(k=0;k<n;k++)
temp=temp+matrix[k][j];
if(temp!=sum)
return false;
}
temp=0;
for(i=0;i<n;i++)
temp=temp+matrix[i][i];
if(temp!=sum)
return false;
temp=0;
for(i=0;i<n;i++)
temp=temp+matrix[i][n-1-i];
if(temp!=sum)
return false;
printf("该方阵为幻方!\n");
return true;
}
void Odd(int n,int matrix[10][10])
{
int i=0,j=n/2;
int number=1;
for(int k=0;k<n*n;k++)
{
matrix[i][j]=number;
i--;
j++;
number++;
if(i<0&&j<n)
{
i=n-1;
}
else if(i>=0&&j>=n)
{
j=0;
}
else if(i<0&&j>=n)
{
if(matrix[n-1][0]!=0)
{
i=i+2;
j=j-1;
}
else
{
i=n-1;
j=0;
}
}
if(matrix[i][j]!=0)
{
i=i+2;
j=j-1;
}
}
}
void DoubleEven(int n,int matrix[10][10])
{
int number=1;
int temp=0;
int i=0,j=0,k=0;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
matrix[i][j]=number++;
for(i=0;i<n;i=i+4)
for(j=0;j<n;j=j+4)
for(k=0;k<4;k++)
{
matrix[i+k][j+k]=n*n+1-matrix[i+k][j+k];
matrix[i+k][j+3-k]=n*n+1-matrix[i+k][j+3-k];
}
}
void SingleEven(int n,int matrix[10][10])
{
int degree=n/2;
int flag=n/4;
int i=0,j=0,k=0;
int temp=0;
int matrix1[10][10]={0};
int matrix2[10][10]={0};
int matrix3[10][10]={0};
int matrix4[10][10]={0};
Odd(degree,matrix1);
for(i=0;i<degree;i++)
for(j=0;j<degree;j++)
{
matrix2[i][j]=matrix1[i][j]+degree*degree;
matrix3[i][j]=matrix1[i][j]+degree*degree*2;
matrix4[i][j]=matrix1[i][j]+degree*degree*3;
}
for(i=0;i<degree;i++)
for(j=0;j<flag;j++)
if(i!=(degree/2))
{
temp=matrix1[i][j];
matrix1[i][j]=matrix4[i][j];
matrix4[i][j]=temp;
}
else
{
temp=matrix1[i][j+degree/2];
matrix1[i][j+degree/2]=matrix4[i][j+degree/2];
matrix4[i][j+degree/2]=temp;
}
for(i=0;i<degree;i++)
for(j=0;j<flag-1;j++)
{
temp=matrix2[i][j+degree/2];
matrix2[i][j+degree/2]=matrix3[i][j+degree/2];
matrix3[i][j+degree/2]=temp;
}
for(i=0;i<degree;i++)
{
for(j=0;j<degree;j++)
matrix[i][j]=matrix1[i][j];
for(k=0;k<degree;k++)
matrix[i][j+k]=matrix3[i][k];
}
for(i=0;i<degree;i++)
{
for(j=0;j<degree;j++)
matrix[i+degree][j]=matrix4[i][j];
for(k=0;k<degree;k++)
matrix[i+degree][j+k]=matrix2[i][k];
}
}
void main()
{
int matrix[10][10]={0};
int n; printf("%d",6%2);
printf("请输入幻方的阶数:");
scanf("%d",&n);
if(n%2!=0)
Odd(n,matrix);
else if(n%4!=0)
SingleEven(n,matrix);
else
DoubleEven(n,matrix);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
printf("%d ",matrix[i][j]);
printf("\n");
}
check(matrix,n);
}
|







