【算法导论】有向图的可达矩阵

​ 有时候，我们关注的不是从一个地点到另一个地点的费用，而是能否从一个顶点到达另一个顶点。因此我们可以假设所有边的权值为单位1，在下面的算法中，我们可以在$O(n^3)$的时间内计算出图中任意两点是否可达，我用可达矩阵来表示有向图中两者是否可达。如果可以从$i$到$j$，则定义$t{ij}=1$,否则$t{ij}=0$。因此我们可以得到下式：

我们以下面的有向图进行具体实现：

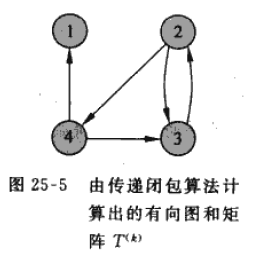
下图给出了计算所得的每一个$T^{(k)}$矩阵：

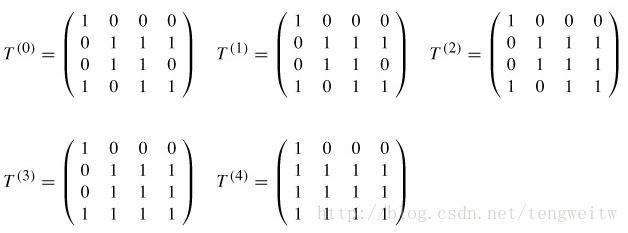
具体程序实现如下：

#include<stdio.h>

#define MAX 10000
#define N 4 //顶点个数

void TransitiveClosure(int dist[N][N],int t[N][N])//寻找可达矩阵
{
	for(int i=0;i<N;i++)//进行遍历
		for(int j=0;j<N;j++)
		{
			if((i==j)||(dist[i][j])==1)//发现可达
				t[i][j]=1;
			else
				t[i][j]=0;
		}

	for(int k=0;k<N;k++)
		for(int i=0;i<N;i++)
			for(int j=0;j<N;j++)
				t[i][j]=t[i][j]||(t[i][k]&&t[k][j]);//由文中公式可得
}

void main()
{
	int dist[N][N]={{1,0,0,0},//邻接矩阵
					{0,1,1,1},
					{0,1,1,0},
					{1,0,1,1}};

	int t[N][N]={0};
	TransitiveClosure( dist, t);
	for(int i=0;i<N;i++)
	{
			for(int j=0;j<N;j++)
				printf("%d ",t[i][j]);
			printf("\n");
	}

}

在上面的程序中，我用了逻辑运算来计算可达矩阵，因为在某些计算机上，对单位的值，逻辑操作的执行速度快于对整数字长数据的算术运算操作，其空间要求也比整数要小。

---

​ 学过图论的可能知道，一个邻接矩阵$A$（若边的权值都为单位$1$）表示两个顶点经过一步的可达情况, $A{ij}$表示经过一步，$i$能到达$j$的次数。同理$A^{(2)}$表示两个顶点经过两部步的可达情况,$A{ij}$表示经过两步，$i$能到达$j$的次数，一次类推……。还是以上面的图为例：

$$A=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 1\\ 0 & 1 & 1 & 0\\ 1 & 0 & 1 & 1 \end{pmatrix} \quad A^{(2)}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 1 & 2 & 3 & 2\\ 0 & 2 & 2 & 1\\ 2 & 1 & 2 & 1 \end{pmatrix}$$

比如$A^{(2)}$中$A_{12}=2$，表示从顶点$2$到顶点$3$经过两步可以到达的次数为$3$。 注意:自己到达自己可以是任意步！

由相关知识可知，可达矩阵$B=A+A^{(2)}+A^{(3)}+\cdots+A^{(n)}$ ，$n$为顶点个数。具体的C​语言实现比上面的算法要复杂，下面用matlab实现：

function P = canget( A )
%计算可达矩阵
%B=A+A^2+A^3+……+A^n   A为邻接矩阵
n=length(A);
P=A;
for i=2:n
    P=P+A^i;
end

P=(P~=0);

结算可以得到相同的结果。由于matlab擅长矩阵运算，因此程序计算十分简单。