【算法导论】单源最短路径之Bellman-Ford算法

​ 单源最短路径指的是从一个顶点到其它顶点的具有最小权值的路径。我们之前提到的广度优先搜索算法就是一种无权图上执行的最短路径算法，即在所有的边都具有单位权值的图的一种算法。单源最短路径算法可以解决图中任意顶点间的最短路径。

​ 对于单源最短路径问题，一般有两种经典解法：

• 对于有权值为负的图，采用Bellman-Ford算法；
• 对于权值全为正的图，常采用Dijkstra算法。本文介绍Bellman-Ford算法，下一篇介绍Dijkstra算法。

Bellman-Ford算法适用于权值可以为负、无权值为负的回路的图，这比Dijkstra算法的使用范围要广。其基本思想为：首先假设源点到所有点的距离为无穷大，然后从任一顶点$u$出发，遍历其它所有顶点$v_i$，计算从源点到其它顶点$v_i$的距离与从$v_i$到$u$的距离的和，如果比原来距离小，则更新，遍历完所有的顶点为止，即可求得源点到所有顶点的最短距离。下面用实例说明：

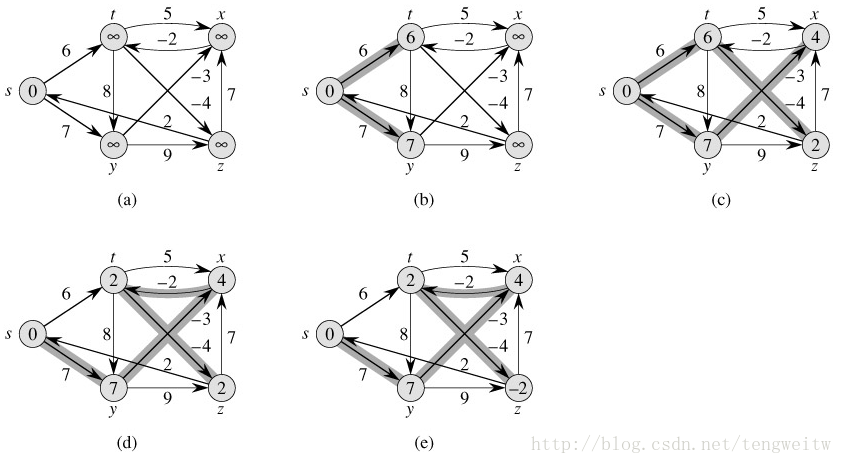
上图中，顶点内的值表示该顶点到s顶点的距离。在下面的具体程序实现中，我用0 1 2 3 4代表 s t x y z.

具体程序实现如下：

#include<stdio.h>
#define M 10//边数
#define N 5//顶点数
#define MAX 10000

int BellmanFord(int dist[N][N],int d[N],int i);

int flag1=0;
int flag2=0;

typedef struct
{
	int startvex;
	int endvex;
	int length;
}edge;
edge T[M];
void main()
{
	int dist[N][N]={{0,6,MAX,7,MAX},
					{MAX,0,5,8,-4},
					{MAX,-2,0,MAX,MAX},
					{MAX,MAX,-3,0,9},
					{2,MAX,7,MAX,0}};//图的邻接矩阵
	int d[N];
	int num=0;
    num=BellmanFord(dist,d, 0);//计算下标为0的顶点到其它顶点的距离，num用于统计边数
	for(int i=0;i<N;i++)//打印到各个顶点之间的距离
		printf("%d ",d[i]);
	printf("\n");
	for(int j=0;j<num;j++)//打印考虑过的边
		printf("start=%d,end=%d,lenth=%d\n",T[j].startvex,T[j].endvex,T[j].length);
}

int BellmanFord(int dist[N][N],int d[N],int i)
{
	for(int j=0;j<N;j++)//初始化
		d[j]=MAX;
	d[i]=0;
	int num=0;

	for(int k=0;k<N-1;k++)
	{
		for(int ii=0;ii<N;ii++)
			for(int jj=0;jj<N;jj++)
			{
				if(dist[ii][jj]!=MAX)
				{
					if(d[jj]>(d[ii]+dist[ii][jj]))//不断更新距离
					{
						d[jj]=d[ii]+dist[ii][jj];//当原节点到jj节点的距离大于
						                         //原节点到ii节点的距离与从ii节点到jj节点的距离和时更新
						T[num].startvex=ii;
						T[num].endvex=jj;
						T[num].length=dist[ii][jj];
						num++;
					}
				}
			}
	}
	for(int ii=0;ii<N;ii++)
	for(int jj=0;jj<N;jj++)//有权值为负的回路的情况
	{
		if(d[jj]>(d[ii]+dist[ii][jj]))
			return 0;
	}
return num;

}

结果显示如下：

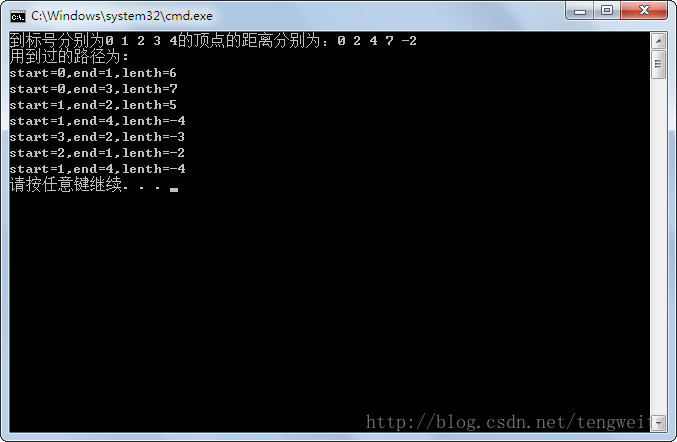
注意：上述的结果与前面图解的一致，但是用到的边有7条比前面图解的阴影部分的边多3条，这是因为图解过程中省略了中间的一些步骤，直接得到最小权值时的情况。通过阴影部分的边，我们可以轻松的找到最短路径所经过的顶点，当然，当图比较复杂时，就该写程序来打印最短路径了。