【算法导论】最小生成树之Kruskal法

​ 在图论中，树是指无回路存在的连通图。一个连通图的生成树是指包含了所有顶点的树。如果把生成树的边的权值总和作为生成树的权，那么权值最小的生成树就称为最小生成树。因为最小生成树在实际中有很多应用，所以我们有必要了解怎样生成最小生成树。构造最小生成树的两种常用方法：Kruskal算法、Prim算法。本文介绍Kruskal算法，Prim算法在下篇文章中介绍。

Kruskal算法是从另一条途径来求网络的的最小生成树。设$G=(V, E)$是一个有$n$个顶点的连通图，则令最小生成树的初值状态为只有$n$个顶点而无任何边的非连通图$T=(V, {\emptyset})$，此时图中每个顶点自成一个连通分量。按照权值递增的顺序依次选择$E$中的边，若该边依附于$T$中两个不同的连通分量，则将此边加入$TE$中，否则舍去此边而选择下一条代价最小的边，直到$T$中所有顶点都在同一连通分量上为止。这时的$T$，便是$G$的一棵最小生成树。

​ 物理老师曾说过，图像比文字的信息量大得多，这可以从一幅图像和一篇文章所占电脑的存储空间大小明显得出。因此我们可以同下面的图解过程了解Kruskal算法的思想：

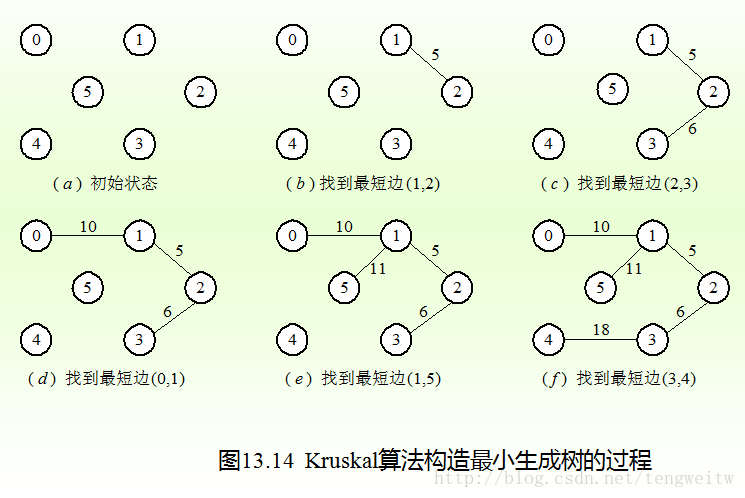
​ 在该算法中，每次都要寻找最短边，如果用邻接矩阵实现的话，则需要对整个矩阵扫描一遍，时间复杂度较高，如果采用邻接表的话，由于每条边都被连接两次，使得寻找时间加倍。所以采用如下结构体：

#include<stdio.h>
#define M 8 //边数
#define N 6  //顶点数 

//图的存储结构体
typedef struct
{
	int startvex,endvex;//边的两个顶点
	int length;//边长
	int sign;//是否被选择,1表示被选择，0表示未被选择，2表示选择后形成环，被抛弃
}edge;
	edge T[M];
	int flag1[N];//标记顶点是否已被选中
void Kruskal(edge T[M],int *flag1)
{
	int i,j,k,l,min;
	int a[M]={0,0,0,1,1,1,2,3,3,4};//边的两个顶点及边的长度
	int b[M]={1,4,5,2,3,5,3,4,5,5};
	int c[M]={10,19,21,5,6,11,6,18,14,33};

	//int a[M]={0,0,0,1,1,2,3,4};//边的两个顶点及边的长度
	//int b[M]={1,3,5,2,4,3,4,5};
	//int c[M]={7,3,5,6,9,8,4,2};
	
	for(i=0;i<N;i++)
		flag1[i]=i;
	for(i=0;i<M;i++)//初始化
	{
		T[i].startvex=a[i];
		T[i].endvex=b[i];
		T[i].length=c[i];
		T[i].sign=0;
	}
	j=0;
	int flag=0;//记录最小边的序号
	while(j<N-1)
	{
		flag=0;
		min=10000;
		for(i=0;i<M;i++)
		{
			if(T[i].sign==0)
			{
				if(T[i].length<min)
				{
					k=T[i].startvex;
					l=T[i].endvex;
					flag=i;
					min=T[i].length;
				}
			}
		}
		T[flag].sign=1;//标记被选中
		//printf("k=%d,l=%d:  ",k,l);

		//printf("\n");
		if(flag1[k]==flag1[l])//当边的两个顶点都已经被选择，说明若选择该边就会形成环
		{
			T[flag].sign=2;//表示抛弃该边
			//printf("ok ");
		}
		else
		{
			j++;
			for(i=0;i<N;i++)
				if(flag1[i]==l)
					flag1[i]=flag1[k];
		}
	//for(int ii=0;ii<M;ii++)
	//	printf(" %d ",T[ii].sign);
	//printf("\n\n");
	}

}

void main()
{

	Kruskal(T,flag1);
	
	for(int i=0;i<M;i++)
		printf("%d ",T[i].sign);
		printf("\n");
}

程序的结果与上面的图解的结果稍有不同，但是正确的，因为最小生成树有时候是不唯一的。