在前面的文章中,我已经讨论了无向图的遍历,现在发现在有向图中,可能会发生无法遍历到所有节点的情况。因此在经历一次深度优先搜索遍历后,如果还存在未被搜索到的节点,则需要再从新的节点开始进行深度优先搜索遍历,直到访问完所有节点。
以下面的有向图为例:
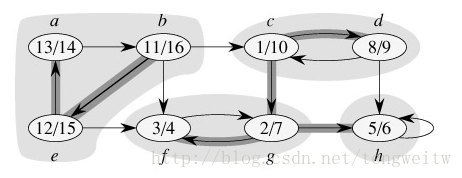
如果从$a$开始进行深度优先搜索遍历,则会得到 $ a b c d h g f $后结束,因此我们还要 从未访问到的节点$e$进行第二次深度优先搜索遍历得到$e$.在前面的深度优先搜索的基础上,有向图的深度优先搜索程序实现如下:
1 |
|
在前面的文章中,我已经讨论了无向图的遍历,现在发现在有向图中,可能会发生无法遍历到所有节点的情况。因此在经历一次深度优先搜索遍历后,如果还存在未被搜索到的节点,则需要再从新的节点开始进行深度优先搜索遍历,直到访问完所有节点。
以下面的有向图为例:

如果从$a$开始进行深度优先搜索遍历,则会得到 $ a b c d h g f $后结束,因此我们还要 从未访问到的节点$e$进行第二次深度优先搜索遍历得到$e$.在前面的深度优先搜索的基础上,有向图的深度优先搜索程序实现如下:
1 | #include<stdio.h> |

微信支付

支付宝