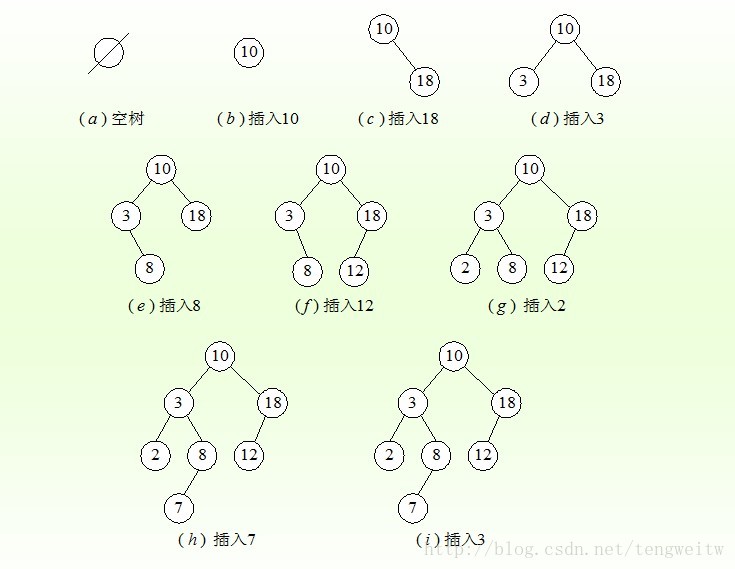
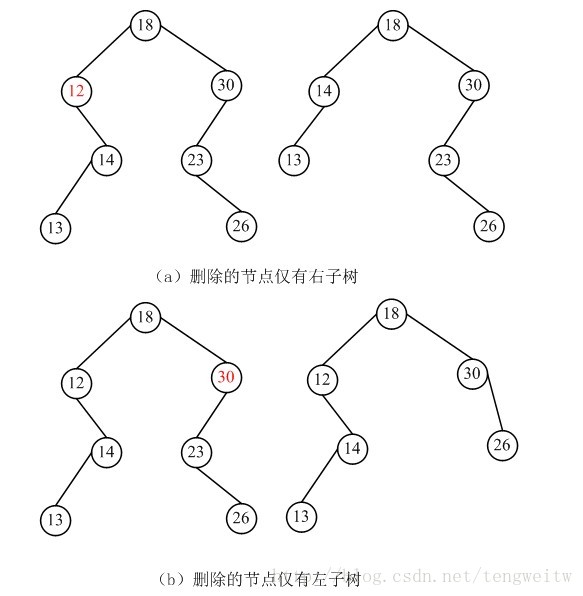
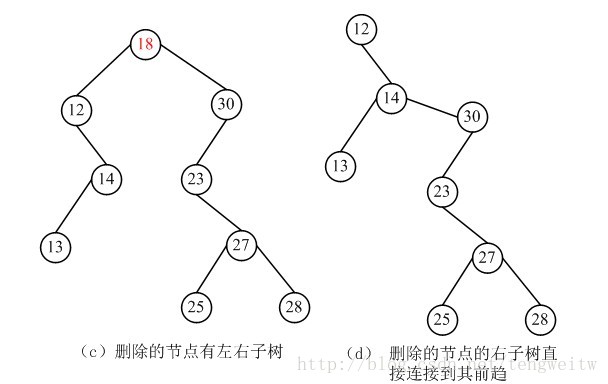
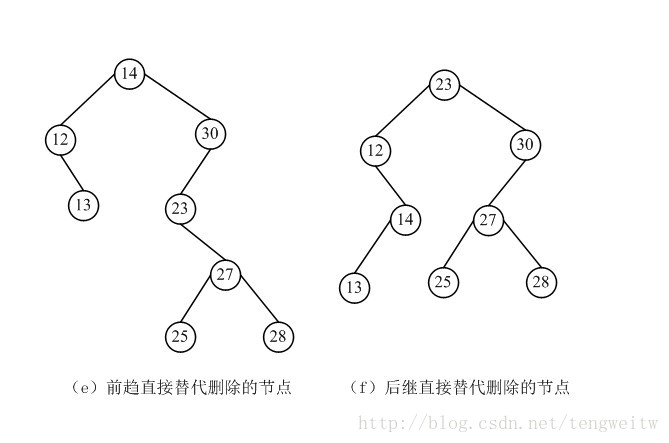
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
| #include<stdio.h>
#include<malloc.h>
#define maxsize 20
typedef struct node
{
int key;
struct node*lchild,*rchild;
}bstnode;
bstnode* InsertBst(bstnode* t,bstnode* s);
bstnode* CreatBst(int* arrayA,int n);
void Layer(bstnode *p);
bstnode* DelBstNode(bstnode* t,int k);
void main()
{
int arrayA[9]={-1,5,2,4,3,1,6,7,8};
int n=sizeof(arrayA)/sizeof(int);
bstnode *head=NULL;
head=CreatBst(arrayA,n);
printf("创建的二叉排序树的广度优先遍历为:\n");
Layer(head);
printf("\n删除内容为5后的二叉排序树的广度优先遍历为:");
head=DelBstNode(head,5);
printf("\n");
Layer(head);
}
bstnode* InsertBst(bstnode* t,bstnode* s)
{
bstnode *f,*p;
p=t;
while(p!=NULL)
{
f=p;
if(s->key<=p->key)
p=p->lchild;
else
p=p->rchild;
}
if(t==NULL)
return s;
if(s->key<f->key)
f->lchild=s;
else
f->rchild=s;
return t;
}
bstnode* CreatBst(int* arrayA,int n)
{
bstnode *t,*s;
t=NULL;
for(int i=1;i<n;i++)
{
s=(bstnode*)malloc(sizeof(bstnode));
s->key=arrayA[i];
s->lchild=s->rchild=NULL;
t=InsertBst(t,s);
}
return t;
}
void Layer(bstnode *p)
{
bstnode* queue[maxsize];
bstnode* s;
int rear=0;
int front=0;
if(p!=NULL)
{
rear=1;
front=0;
queue[rear]=p;
while(front<rear)
{
front++;
s=queue[front];
printf("%d ",s->key);
if(s->lchild!=NULL)
{
rear++;
queue[rear]=s->lchild;
}
if(s->rchild!=NULL)
{
rear++;
queue[rear]=s->rchild;
}
}
}
}
bstnode* DelBstNode(bstnode* t,int k)
{
bstnode *p,*q,*s,*f;
p=t;
q=NULL;
while(p!=NULL)
{
if(p->key==k) break;
q=p;
if(p->key<k)
p=p->rchild;
else
p=p->lchild;
}
if(p==NULL)
{
printf("\n没有找到该节点\n");
return t;
}
if(p->lchild==NULL)
{
if (q==NULL)
t=p->rchild;
else if (q->lchild==p)
q->lchild=p->rchild;
else q->rchild=p->rchild;
free(p);
}
else
{
f=p; s=p->lchild;
while(s->rchild!=NULL )
{
f=s;
s=s->rchild;
}
if ( f==p )
f->lchild=s->lchild;
else f->rchild=s->lchild;
p->key=s->key;
free(s);
}
return t;
}
|