快速排序的最坏运行时间为O(n2),虽然这最坏情况的时间复杂度比较大,但快速排序通常是用于排序的最佳实用选择,这是因为其平均性能相当好,平均时间复杂度为O(nlogn),并且O(nlogn)中的隐含常数因子很小。另外,它能够进行就地排序,因此在虚拟内存中也能较好的运行。
快速排序算法的性能:其运行时间与划分是否对称有关,而是否对称与主元的选取有关。从渐进的意义上讲,如果对称,就和合并的算法一样快,如果不对称,就和插入排序算法一样慢。需要注意的是,但每次递归是都是按照常数比例划分时,从渐进意义上看,与对称划分效果一样,都是O(nlogn).
和合并排序一样,快速排序也是基于分治模式的。分治过程分为三个步骤:分解、解决、合并。
快速合并的基本思想:从要排序的序列中,随意取一个值作为主元,从而将序列以此分为大于和小于主元的两个子序列,然后重复上述过程(递归调用)。
下面以一个分解过程为例:
假设要排序的序列为:2、8、7、1、3、5、6、4。首先,随便选取主元,在这里我们选择4;其次,通过分解将原序列分为子序列2、1、3和子序列7、5、6、8;最后分别以两个子序列为原序列,不断重复上述过程。分解过程的图解如下:
图1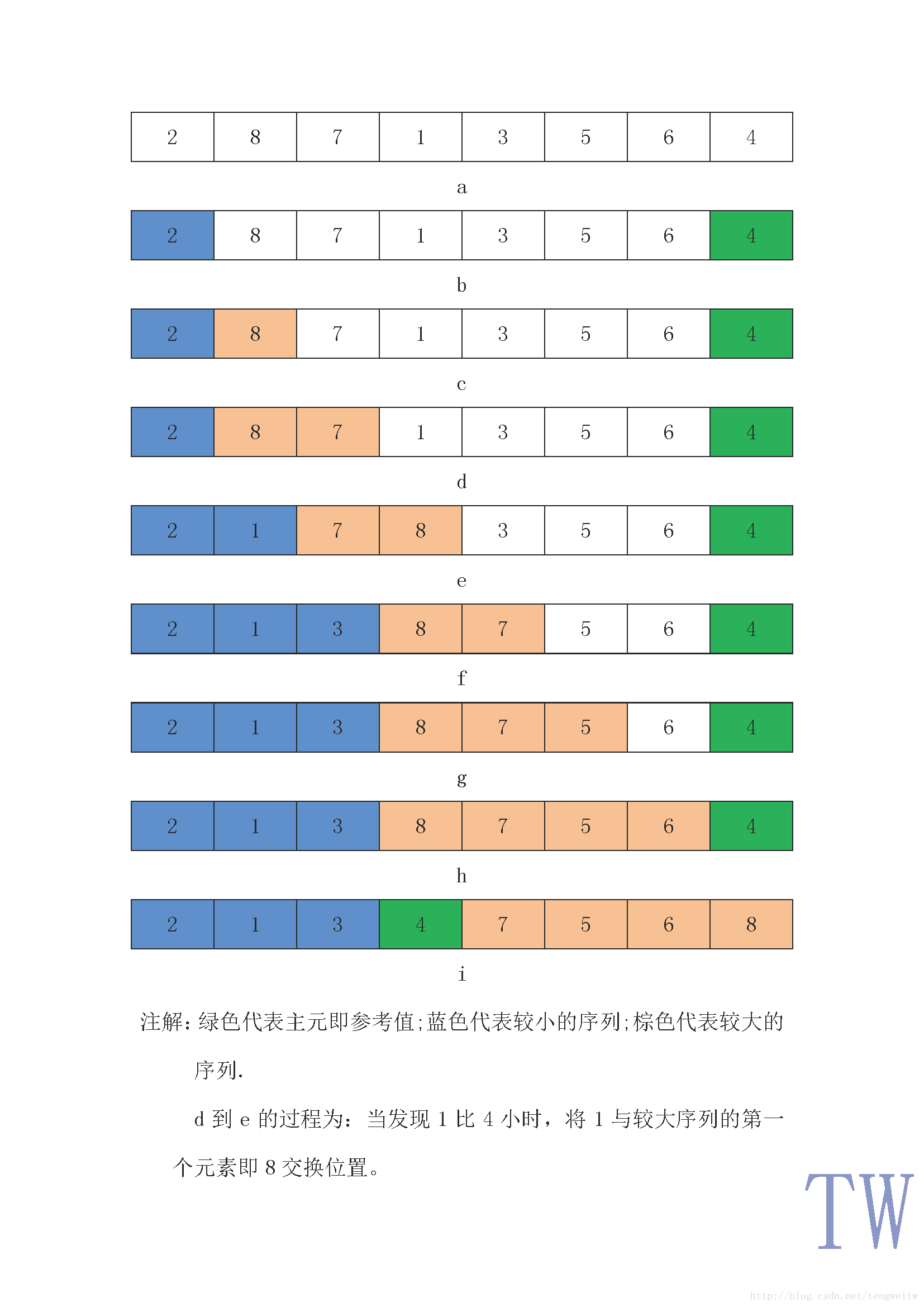
具体实现如下:
分解过程:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27/**************************************************\
函数功能:将原数组分成全大于和全小于x的两个子数组
输入:原始数组、要对数组进行操作的起始和结束下标
输出:x在数组中的位置
\**************************************************/
int Partition(int*Array,int n,int p,int r)
{
int x=Array[r];
int i=p-1;
int temp=0;
for(int j=p;j<=r-1;j++)
{
if(Array[j]<=x)
{
i++;
temp=Array[i];
Array[i]=Array[j];
Array[j]=temp;
}
}
temp=Array[i+1];
Array[i+1]=Array[r];
Array[r]=temp;
return i+1;
}递归过程:
1 | /**************************************************\ |
完整实例:
1 |
|

