堆排序像合并排序一样,时间复杂度为$O(nlogn)$;像插入排序一样,是一种原地排序(在任何时候只有常数个元素存储在数组外)。
二叉堆的概念:是一种数组对象,可以被视为一棵完全二叉树,树的每一层都是填满的,最后一层可能除外。
二叉树有两种:最大堆和最小堆。最大堆:父节点不小于子节点。最小堆:父节点不大于子节点。在堆排序中我们使用最大堆;最小堆通常在构造优先队列时使用。
进行堆排序分为三个模块:1.保持最大堆性质;2.建堆;3:进行排序。
保持最大堆性质
以下图为例,使以$i$为根的子树成为最大堆:
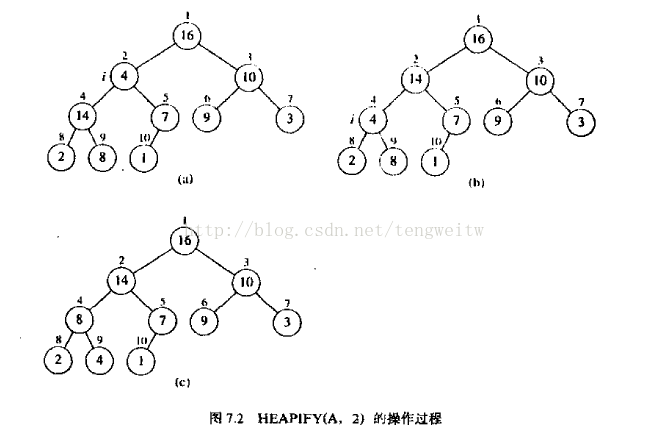
具体程序如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
void MaxHeapify(int* arrayA,int n,int i)
{
int Length=n;
int l=2*i;
int r=l+1;
int largest=0;
int temp=0;
if((l<Length)&&(arrayA[l]>arrayA[i]))
largest=l;
else
largest=i;
if((r<Length)&&(arrayA[r]>arrayA[largest]))
largest=r;
if(largest!=i)
{
temp=arrayA[i];
arrayA[i]=arrayA[largest];
arrayA[largest]=temp;
MaxHeapify(arrayA,n,largest);
}
}
|
建堆:使数组arrayA中的元素成为最大堆
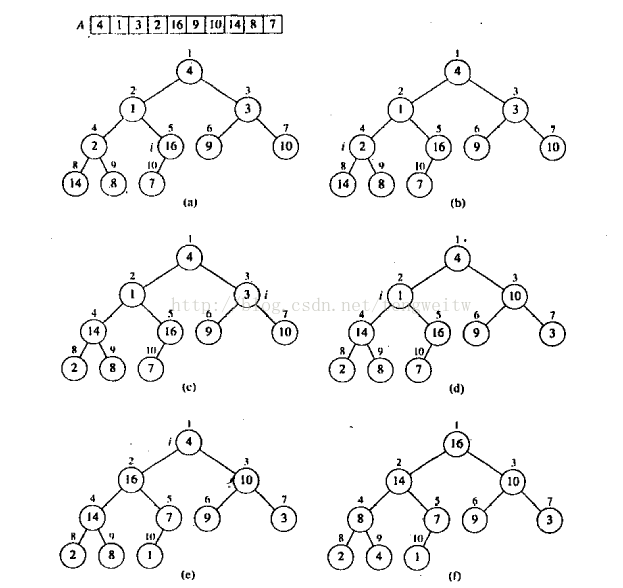
具体程序如下:
1
2
3
4
5
6
7
8
9
10
|
void BuildMaxHeap(int* arrayA,int n)
{
for(int i=n/2;i>0;i--)
MaxHeapify(arrayA,n,i);
}
|
堆排序
主要思想是将每次的堆的顶节点与最末的叶节点进行交换,然后重新根据最大堆性质使得顶节点(根)成为最大值,如此循环。
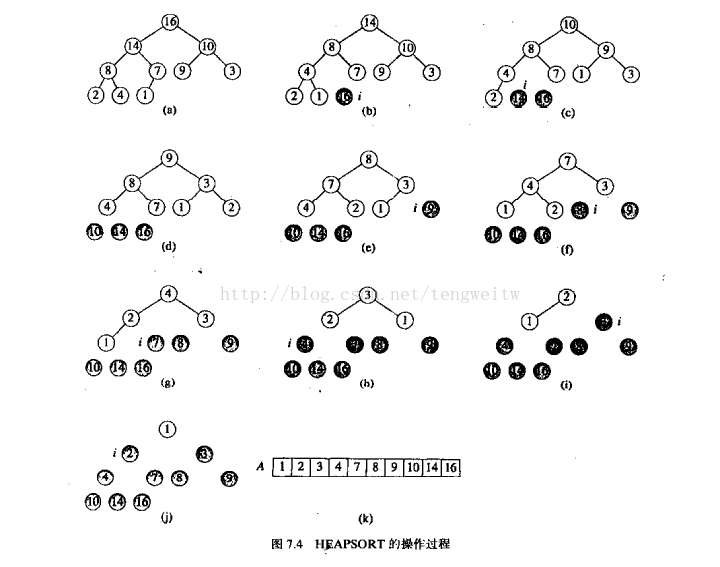
具体程序如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
void HeapSort(int* arrayA,int n)
{
int temp=0;
int Length=n;
for(int i=Length-1;i>=2;i--)
{
temp=arrayA[1];
arrayA[1]=arrayA[i];
arrayA[i]=temp;
n--;
MaxHeapify(arrayA,n,1);
}
}
|
下面将三个步骤综合起来,总的排序算法程序如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
| #include<iostream>
#include<ctime>
using namespace std;
void MaxHeapify(int* arrayA,int n,int i);
void BuildMaxHeap(int* arrayA,int n);
void HeapSort(int* arrayA,int n);
void main()
{
int arrayA[11]={0,4,1,3,2,16,9,10,14,8,7};
int Length=sizeof(arrayA)/sizeof(int);
BuildMaxHeap(arrayA,Length);
cout<<"原序列为:";
for(int i=0;i<Length;i++)
cout<<arrayA[i]<<" ";
cout<<endl;
HeapSort(arrayA,Length);
cout<<"排序好的序列为:";
for(int i=0;i<Length;i++)
cout<<arrayA[i]<<" ";
cout<<endl;
}
void MaxHeapify(int* arrayA,int n,int i)
{
int Length=n;
int l=2*i;
int r=l+1;
int largest=0;
int temp=0;
if((l<Length)&&(arrayA[l]>arrayA[i]))
largest=l;
else
largest=i;
if((r<Length)&&(arrayA[r]>arrayA[largest]))
largest=r;
if(largest!=i)
{
temp=arrayA[i];
arrayA[i]=arrayA[largest];
arrayA[largest]=temp;
MaxHeapify(arrayA,n,largest);
}
}
void BuildMaxHeap(int* arrayA,int n)
{
for(int i=n/2;i>0;i--)
MaxHeapify(arrayA,n,i);
}
void HeapSort(int* arrayA,int n)
{
int temp=0;
int Length=n;
for(int i=Length-1;i>=2;i--)
{
temp=arrayA[1];
arrayA[1]=arrayA[i];
arrayA[i]=temp;
n--;
MaxHeapify(arrayA,n,1);
}
}
|
注意:我是在vs2008上运行的,与vc 6.0有点区别,主要是循环体中的循环变量的作用域,出错体现在循环变量的重复定义上。例如:在vs2008或vs2010上,程序为:
#include
void main()
{
int i=0;
for(int i=0;i<5;i++)
printf(“%d “,i);
}
则在VC 6.0上需改为:
#include
void main()
{
int i=0;
for(i=0;i<5;i++)
printf(“%d “,i);
}




