【图解例说机器学习】线性回归

线性回归之于机器学习，正如Hello World之于编程语言，也如MINST之于深度学习。

首先，我们先定义一些即将用到的数学符号：

Notations	Meaning	Notations	Meaning
$M$	Number of parameters $\mathrm w$	$N$	Number of instances
$\mathrm X={\mathrm x_1,\mathrm x_2,\cdots,\mathrm x_N}^{\mathrm T}$	$N\times M$ matrix for training	$D$	Number of features
$\mathrm y={y_1,y_2,\cdots,y_N}^\mathrm{T}$	Set of targets	$y_i$	Target of instance $i$
$\mathrm{x}_i={x_i^{(1)},x_i^{(2)},\cdots,x_i^{(D)}}^\mathrm{T}$	Set of features for instance $i$	$x_i^{(j)}$	Feature $j$ for instance $i$
$\mathrm w={\omega_1,\omega_2,\cdots,\omega_M}^\mathrm{T}$	Weights of input $\mathrm x$	$\omega_i$	Weight of feature $i$
$\phi={\phi_1,\phi_2,\cdots,\phi_M}^\mathrm{T}$	Set of functions	$\phi_i(\mathrm x)$	Function of features

模型描述

在线性回归中，假设目标值与参数 $\mathrm{w}={\omega_n}$之间线性相关，通过构建损失函数$E$，求解损失函数最小时的参数。也就是说，线性回归试图学习得到如下函数：

$\hat y=\omega_0+\sum\limits_{j=1}^{M}\omega_j\phi_j(\mathrm x)=\omega_0+\mathrm w^{\mathrm T}\phi(\mathrm x)\tag{1}$

公式(1)是线性回归模型的一般形式，看起来不是那么直观。其常见的形式如下：

当$D=1,\phi_j(x)=x^j$时，公式(1)可以表示为：
$\hat y=\omega_0+\omega_1x+\omega_2x^2+\cdots+\omega_Mx^M\tag{2}$
此时，线性回归就变成了多项式回归。
当$D=M,\phi_j(\mathrm x)=x^{(j)}$时，公式(1)可以表示为：
$\hat y=\omega_0+\omega_1x^{(1)}+\omega_2x^{(2)}+\cdots+\omega_Mx^{(M)}\tag{3}$
此时，线性回归就变成了我们通常所说的线性回归—-多元一次方程。当只有一维特征($M=1$) 时，可以得到我们初中就学过的一元一次方程

$\hat y=\omega_1x+\omega_0\tag{4}$

为使本文通俗易懂，除非作特别说明，本文仿真都以这个一元一次方程为例介绍线性回归

代价函数

线性回归的目的就是使得我们预测得到的$\hat y$与真实值$y$之间的误差最小。这里的误差可以用不同的距离度量，这里我们使用平方和。此时，代价函数就可以表示为

$E=\sum\limits_{i=1}^N{(\hat y_i-y_i)^2}=\sum\limits_{i=1}^N{(\omega_0+\mathrm w^{\mathrm T}\phi(\mathrm x_i)-y_i)^2}=\sum\limits_{i=1}^{N}{[\omega_0+\sum\limits_{j=1}^{M}{\omega_j\phi_j(\mathrm{x}_i)-y_i]^2}}\tag{5}$

下面我们在二维空间($M=1$)和三维空间($M=2$)画出代价函数图像。这里我们假定$\phi_i(\mathrm x)=x^{(i)}$，$\omega_0,\omega_1,\omega_2$已知，则公式(1)可以分别表示为：

$\hat y=\omega_0+\omega_1x^{(1)}\tag{6}$ $\hat y=\omega_0+\omega_1x^{(1)}+\omega_2x^{(2)}\tag{7}$

根据公式(6),(7)，我们可以得到图1和图2中的直线和二维平面：

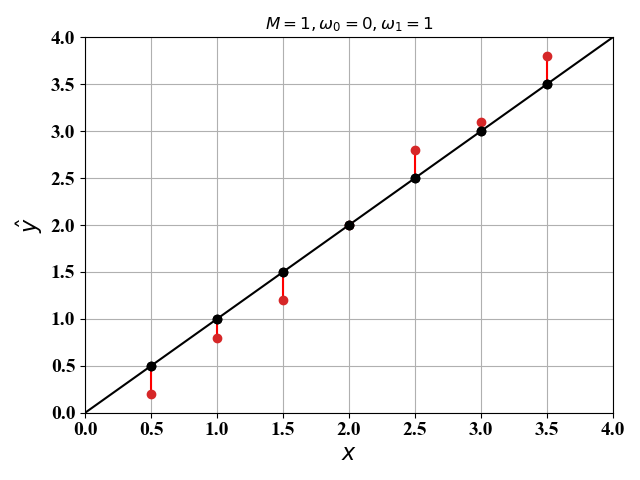
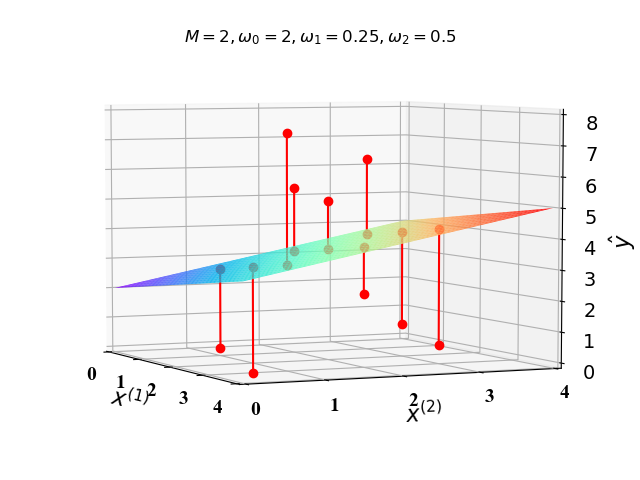
图1和图2中的红色的点是 $\mathrm x$ 对应的真实值 $\mathrm y$ ，红色线段即为误差值。

一个例子

图1和图2展示的是给定参数$\omega_0,\omega_1,\omega_2$下的真实值$y$与预测值$\hat { y}$的误差。不同的参数可以得到不同的误差值，线性回归的目的就是寻找一组参数是的误差最小。下面我们通过图3和图4来说明：

我们假设训练集有3组数据$(x, y)$：$(1, 0.8) (2, 2) (3, 3.1)$ 。我们这里使用一元线性回归，即公式(6)，此时线性回归的目的就是找到一条直线$\hat y=\omega_1x+\omega_0$使得这3组数据点离直线最近。

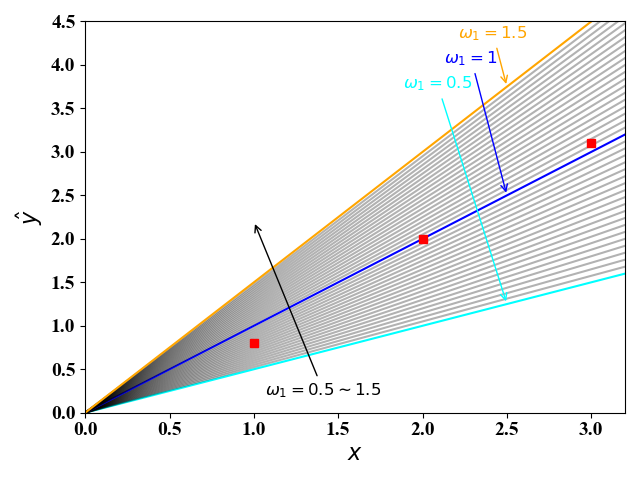
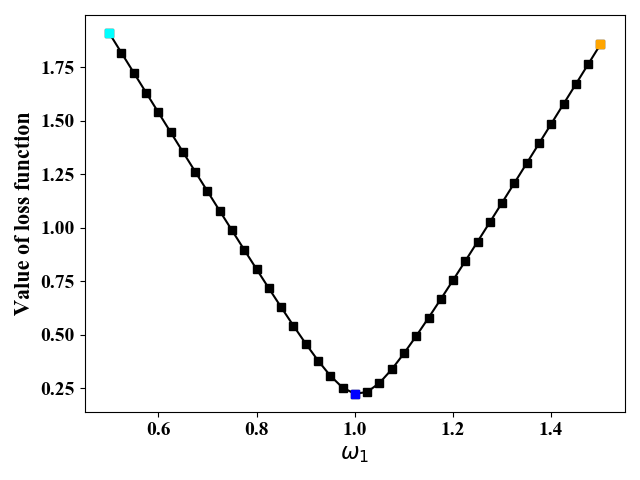
图3画出了当$\omega_0=0,\omega_1=0.5\sim1.5$时，直线$\hat y=\omega_1x+\omega_0$的图像。图4给出了当$\omega_1$取不同值时，代价函数值的变化。从图3和图4可以看出，当$\omega_1=1$时，代价最小。

正规方程与梯度下降

线性回归的本质就是解如下优化问题：

$\min\limits_{\mathrm w}\quad E=\sum\limits_{i=1}^{N}{[\omega_0+\sum\limits_{j=1}^{M}{\omega_j\phi_j(\mathrm{x}_i)-y_i]^2}}\tag{8}$

令$\bar{\mathrm w}={\omega_0,\mathrm w},\bar{\phi}={\phi_0,\phi},\phi_0(\mathrm x)=1$，并将问题(8)表示成向量相乘的形式：

$\min\limits_{\mathrm {\bar w}}\quad E=[\bar\phi(\mathrm X)\mathrm{\bar w}-\mathrm y]^{\mathrm T}[\bar\phi(\mathrm X)\mathrm{\bar w}-\mathrm y]\tag{9}$

公式(9)中，$\bar{\phi}(\mathrm X)$是一个$N\times M+1$维的矩阵:

$\bar\phi(\mathrm X)= \left\{\begin{matrix} \phi_0(\mathrm x_1) & \phi_1(\mathrm x_1) & \cdots & \phi_M(\mathrm x_1)\\ \phi_0(\mathrm x_2) & \phi_1(\mathrm x_2) & \cdots & \phi_M(\mathrm x_2)\\ \vdots & \vdots & \cdots &\vdots \\ \phi_0(\mathrm x_N) & \phi_1(\mathrm x_N) & \cdots & \phi_M(\mathrm x_N) \end{matrix} \right\}\tag{10}$

通过求表达式(8)的Hessian矩阵，可以知道这是一个凸优化问题。那么问题就变得十分简单了，可以用现成的工具来求解：比如CVX, CPLEX, MATLAB等等。这些解法器一般都是通过梯度法(后面会讲解)来求解问题的。当然我们也可以通过凸问题的性质，得到其解析解。

正规方程法

由于误差函数(8)是一个凸函数，所以其导数为0的点就是最优点。为此，我们将$E$对$\mathrm{\bar w}$进行微分求导入下：

$\frac{\partial{E}}{\partial{\mathrm{\bar w}}}=\bar\phi^{\mathrm T}(X)[\bar\phi(\mathrm X)\mathrm{\bar w}-\mathrm y]=0\tag{11}$ $\bar\phi^{\mathrm T}(X)\bar\phi(\mathrm X)\mathrm{\bar w}=\bar\phi^{\mathrm T}(\mathrm X)\mathrm y\rightarrow\mathrm{\bar w}=[\bar\phi^{\mathrm T}(X)\bar\phi(\mathrm X)]^{-1}\bar\phi^{\mathrm T}(\mathrm X)\mathrm y\tag{12}$

由公式(11)可知，给定训练数据$\mathrm X$，我们就可以求出最佳的$\mathrm{\bar w}$。需要注意的是，这里需要求矩阵的逆，计算量比较大，不适合当训练数据较大的情况。这时我们可以通过梯度下降法来求解。

梯度下降法

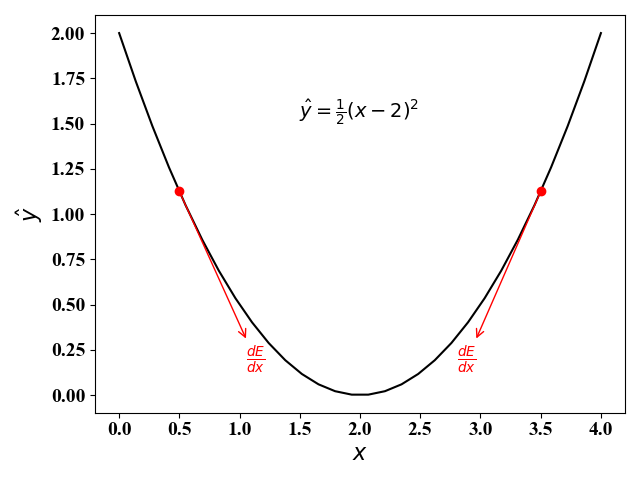
使用梯度下降法，可以对凸问题求得最优解，对非凸问题，可以找到局部最优解。梯度下降法的算法思想如下图5和图6所示：

在左图(图5)中，梯度为$\frac{d\hat y}{d x}=x-2$。当$x<2$时，梯度小于零，此时$x$应当向右移动来减小函数值(负梯度方向)；当$x>2$时，梯度大于零，此时$x$应当向左移动来减小函数值(负梯度方向)。
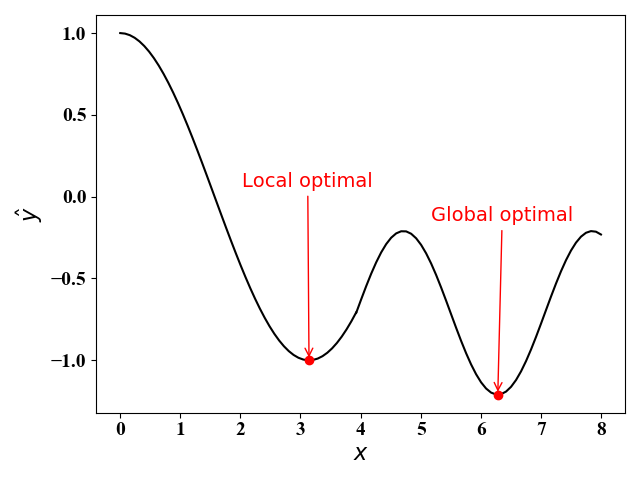
在右图(图6)中，函数不是凸函数的情况下，使用梯度下降法会得到局部最优解(假定初始值为$x=0$)。当初始值$x=7$时，我们可以得到最优解。因此，初始值对梯度下降法影响较大，我们可以通过随机选择初始值来克服陷入局部最优解的情况。

根据(10)得到的梯度表达式，梯度下降的每一次迭代过程如下：

$\bar{\mathrm w}^{t+1}=\bar{\mathrm w}^{t}-\eta\frac{\partial{E}}{\partial{\mathrm{\bar w}}}=\bar{\mathrm w}^{t}-\eta\bar\phi^{\mathrm T}(X)[\bar\phi(\mathrm X)\mathrm{\bar w}-\mathrm y]\tag{13}$

将公式(13)的矩阵相乘展开可以得到

$\omega_j^{t+1}=\omega_j^t-\eta\sum\limits_{i=1}^{N}{[\omega_0+\sum\limits_{j=1}^{M}{\omega_j\phi_j(\mathrm{x}_i)-y_i]}\phi_j(\mathrm x_i)}\tag{14}$

公式(13)或(14)就是标准的梯度下降法，其中$\eta$是每次迭代的步长大小。

$\eta$较小时，迭代较慢，当时可以保证收敛到最优解(凸函数的情况下)；$\eta$较大时，函数值下降较快，但容易发生震荡。
每次迭代时，需要使用所有的样本点$\mathrm x_i,i=1,2,\cdots,N$。当数据样本点非常大时，开销十分大。

为此，有人提出了随机梯度下降，其迭代公式如下：

$\omega_j^{t+1}=\omega_j^t-\eta{[\omega_0+\sum\limits_{j=1}^{M}{\omega_j\phi_j(\mathrm{x_i})-y_i]}\phi_j(\mathrm x_i)}\tag{15}$

随机梯度下降又称连续梯度下降，比较适合于实时系统，即整个数据集$\mathrm x_i$不是可以一次性获得的，但是我们需要作出预测的场景。相较于梯度下降法(14)，随机梯度只根据当前样本更新迭代，随机性较大。因此有可能跳出标准梯度下降法的局部最优解。

算法实现

这里我们使用sklearn中波士顿房价的数据集，该数据集有13维特征，506个样例。为简便起见，我们只取前2维特征作为输入($M=D=2,\hat y=\omega_0+\omega_1x^{(1)}+\omega_2x^{(2)}$)，前500个作为输入样例，后6个作为预测样例。在算法实现中，我们分别考虑了正规方程法和梯度下降法。并且，考虑到$x^{(1)}$和$x^{(2)}$的取值范围差距较大，我们还考虑了特征值缩放。为此，我们实现了上述四种算法的组合[特征不缩放(特征缩放)+正规方程法(梯度下降法)]。

算法结果

图7给出了上述4种算法的结果：

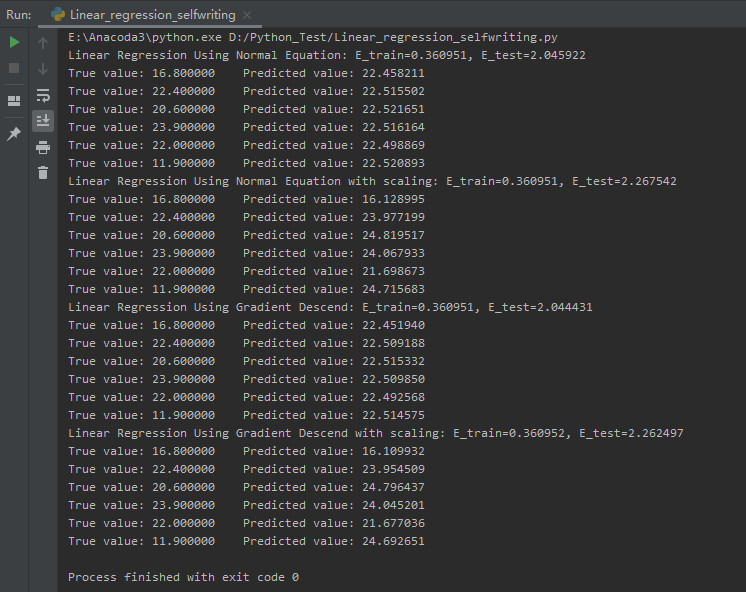
图7中，E_train为训练误差，即前500个样例的真实值与预测值的误差，E_test为预测误差，即最后6个样例的真实值与预测值的误差。由于误差函数对于参数w是凸函数，我们总能得到最优解，即最小的训练误差，所以上述四种方法的训练误差相同。

特征缩放与梯度下降法

图7能得到最小误差函数值，是因为目标函数$E$是参数$\omega_1$和$\omega_2$的凸函数。为方便起见，对于具体实例，我们给出$E$的表达式：

$E(\omega_0,\omega_1,\omega_2)=\sum\limits_{i=1}^{500}(\omega_0+\omega_1*x^{(1)}+\omega_2*x^{(2)}-y_i)^2\tag{16}$

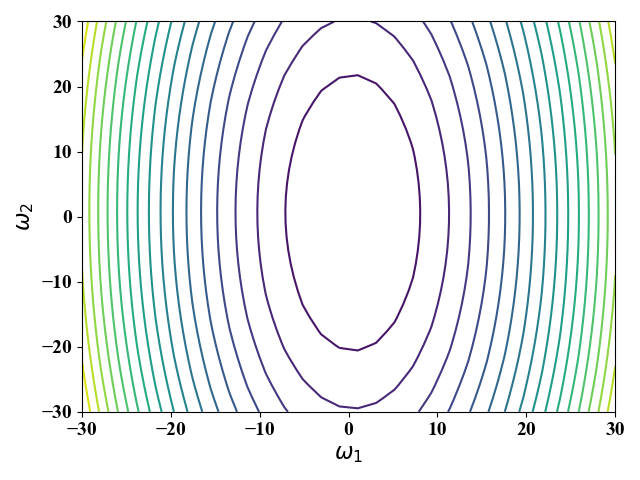
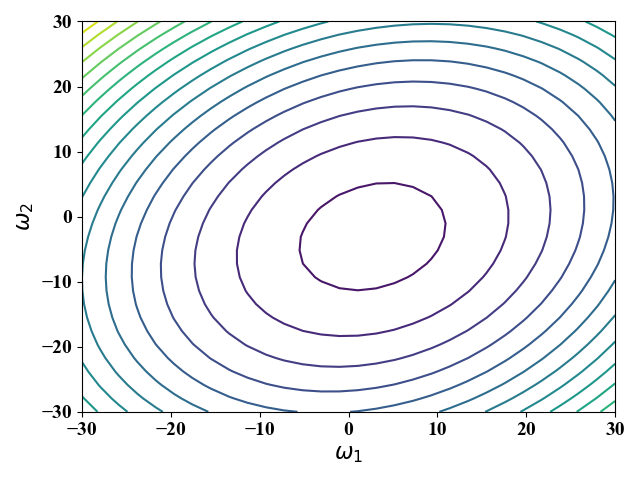
公式(16)中，$\omega_0$与具体样例无关，$\omega_0$的值不改变$E$的图像形状，改变$\omega_0$相当于进行位移，我们这里假定$\omega_0=0$。为此，当给定波士顿房价数据集，即$x^{(1)},x^{(2)},y_i$ 给定时，我们可以画出公式(16)对应的等高线图，图8。

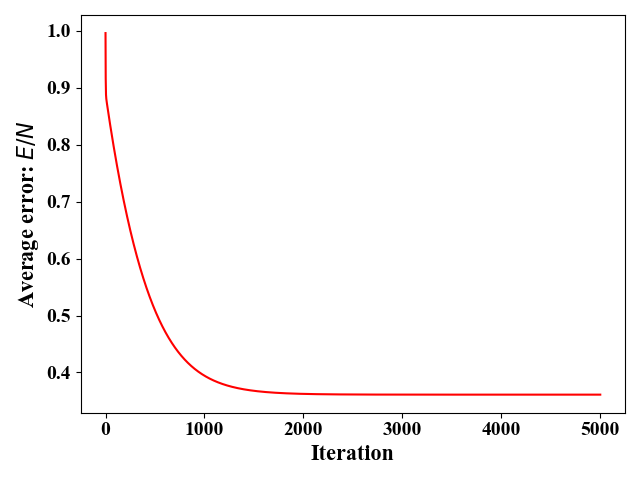
从图8可以看出，当改变$\omega_2$时，$E$变的较快(等高线在$\omega_2$方向较为稀疏)。这是因为$\omega_2$的系数为$x^{(2)}$，而$x^{(2)}$相对于$x^{(1)}$有较大的取值。在这种情况下，对梯度下降法就十分不友好—很容易跳过最优解。也就是说，步长设置要十分小，这就会导致收敛速度慢。在我们这个实例中，步长最大只能设置为$\eta=5e^{-6}$，此时需要差不多30000次迭代才能收敛到最优，如图10所示。
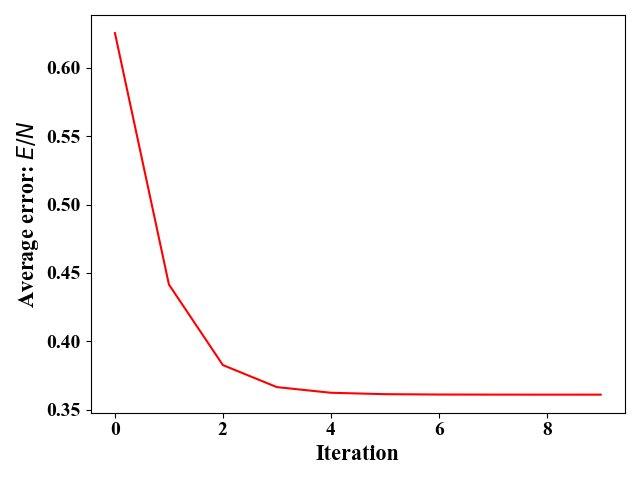
特征缩放是一种解决上述情况下，梯度下降法收敛慢的方法。特征缩放的表达式都十分简单，这里不再赘述，我们这里是直接使用的sklearn库中的preprocessing.StandardScaler()函数对样例进行特征缩放。对$x^{(1)},x^{(2)}$缩放后，我们可以用相同的方式画出对应的等高线图，图9，以及收敛图，图11。经过特征缩放后，图9中等高线在$\omega_1,\omega_2$方向上的稀疏程度差不多。图11中，步长可以设置得较大($\eta=1e^{-3}$)，收敛速度变得极快，只需要迭代8次左右就达到最优。

附录

下面给出图1—图11的Python源代码如下：

图1和图2的python源代码:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


# Set the format of labels
def LabelFormat(plt):
    ax = plt.gca()
    plt.tick_params(labelsize=14)
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    font = {'family': 'Times New Roman',
            'weight': 'normal',
            'size': 16,
            }
    return font


# 2-d case
omega_0 = 0
omega_1 = 1
data_train = [[0.5, 0.2], [1, 0.8], [1.5, 1.2], [2, 2], [2.5, 2.8], [3, 3.1], [3.5, 3.8]]
x_train = [d[0] for d in data_train]
y_train = [d[1] for d in data_train]

x = np.linspace(0, 4, 30).reshape(30, 1)
y = omega_1 * x + omega_0

x_test = x_train
y_test = y_train
y_hat = omega_1 * x_test

plt.figure()
plt.plot(x, y, 'k-')
for i in range(len(x_test)):
    plt.stem([x_test[i], ], [y_test[i], ], linefmt='rx', bottom=y_hat[i], basefmt='ko', markerfmt='C3o',
             use_line_collection=True)
# Set the labels
font = LabelFormat(plt)
plt.xlabel('$x$', font)
plt.ylabel('$\hat y$', font)
plt.title('$M=1,\omega_0=0,\omega_1=1$')
plt.xlim(0, 4)
plt.ylim(0, 4)
plt.grid()

plt.show()

# 3-d case
omega_0 = 2
omega_1 = 0.25
omega_2 = 0.5


x1 = np.linspace(0, 4, 30).reshape(30, 1)
x2 = np.linspace(0, 4, 30).reshape(30, 1)

X1, X2 = np.meshgrid(x1, x2)
y_hat = omega_0 + omega_1 * X1 + omega_2 * X2
fig = plt.figure()
ax = fig.gca(projection='3d')

x1_test=np.array([1,2,3])
x2_test=np.array([1,2,3])
X1_test, X2_test = np.meshgrid(x1_test, x2_test)

y_test = omega_0 + omega_1 * X1_test + omega_2 * X2_test+8*np.random.rand(3,3)-4

ax.plot_surface(X1, X2, y_hat, cmap='rainbow')

for i in range(len(x1_test)):
    for j in range(len(x2_test)):
        y_predict= omega_0 + omega_1 * x1_test[i] + omega_2 * x2_test[j]
        ax.plot([x1_test[i],x1_test[i]],[x2_test[j],x2_test[j]],[y_test[i][j],y_predict],'r-o')

# Set the labels
font = LabelFormat(plt)
ax.set_xlabel('$x^{(1)}$', font)
ax.set_ylabel('$x^{(2)}$', font)
ax.set_zlabel('$\hat y$', font)
ax.set_xlim(0, 4)
ax.set_ylim(0, 4)
ax.set_zlim(0, 8)
ax.set_xticks([0,1,2,3,4])
ax.set_yticks([0,1,2,3,4])
ax.set_title('$M=2,\omega_0=2,\omega_1=0.25,\omega_2=0.5$')

# Customize the view angle so it's easier to see that the scatter points lie
ax.view_init(elev=5., azim=-25)
plt.show()

图3和图4的python源代码:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import matplotlib as mpl
import math


# Set the format of labels
def LabelFormat(plt):
    ax = plt.gca()
    plt.tick_params(labelsize=14)
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    font = {'family': 'Times New Roman',
             'weight': 'normal',
             'size': 16,
             }
    return font


# Plot the training points: different
def PlotTrainPoint(X):
    for i in range(0, len(X)):
        plt.plot(X[i][0], X[i][1], 'rs', markersize=6, markerfacecolor="r")


# Loss function--Square Error function
def LossFunction(Y, predictedY):
    lengthY = len(Y)
    error = 0
    for i in range(lengthY):
        error += pow(Y[i] - predictedY[i], 2)

    return math.sqrt(error)


trainData = [[1, 0.8], [2, 2], [3, 3.1]]

# Predicted function: y=\omega_1*x+\omega_0 Here \omega_0 is assumed to be 0 for simplifcity

x = np.linspace(0, 4, 30).reshape(30, 1)
omega_1 = np.linspace(0.5, 1.5, 41).reshape(41, 1)
omega_0 = 0
y_hat = []
#Get the value of x and y in the trainData
x_train = [d[0] for d in trainData]
y_train = [d[1] for d in trainData]
error_all = []

# Plot the figure to show the function: y=\omega_1*x+\omega_0
for i in range(len(omega_1)):
    y_hat.append(omega_1[i] * x)
    if omega_1[i]==0.5:
        plt.plot(x, y_hat[i],  color='cyan', alpha=1)
    elif omega_1[i]==1:
        plt.plot(x, y_hat[i], color='blue', alpha=1)
    elif omega_1[i]==1.5:
        plt.plot(x, y_hat[i], color='orange', alpha=1)
    else:
        plt.plot(x, y_hat[i], color='black', alpha=0.3)
    # Compute the errors for each omega_1
    error_all.append(LossFunction(y_train, omega_1[i].T*x_train+omega_0))

# Set the axis
font=LabelFormat(plt)
PlotTrainPoint(trainData)
# Label the critical points
plt.annotate('$\omega_1=1.5$', xy=(2.5, 2.5*1.5), xycoords='data',
             xytext=(-35, 35), textcoords='offset points', color='orange', fontsize=12, arrowprops=dict(arrowstyle="->",
             connectionstyle="arc,rad=90", color='orange'))
plt.annotate('$\omega_1=1$', xy=(2.5, 2.5*1), xycoords='data',
             xytext=(-45, 95), textcoords='offset points', color='b', fontsize=12, arrowprops=dict(arrowstyle="->",
             connectionstyle="arc,rad=90", color='b'))
plt.annotate('$\omega_1=0.5$', xy=(2.5, 2.5*0.5), xycoords='data',
             xytext=(-75, 155), textcoords='offset points', color='cyan', fontsize=12, arrowprops=dict(arrowstyle="->",
             connectionstyle="arc,rad=90", color='cyan'))

plt.annotate('$\omega_1=0.5\sim 1.5$', xy=(1, 2.2), xycoords='data',
             xytext=(8, -125), textcoords='offset points', color='k', fontsize=12, arrowprops=dict(arrowstyle="->",
             connectionstyle="arc,rad=90", color='k'))
plt.xlabel('$x$',font)
plt.ylabel('$\hat y$',font)
plt.xlim([0,3.2])
plt.ylim([0,4.5])
plt.show()

# Show the error when omega_1 changes
plt.figure()
font=LabelFormat(plt)
plt.plot(omega_1,error_all, 'k-s')
error_min=min(error_all)
index_min=error_all.index(error_min)
print(index_min)
# plot the error at the given three point
plt.plot(omega_1[index_min],error_min,'bs')
plt.plot(omega_1[0],error_all[0],'cyan',marker='s')
plt.plot(omega_1[-1],error_all[-1],'orange',marker='s')

plt.xlabel('$\omega_1$', font)
plt.ylabel('Value of loss function', font)
plt.show()

图5和图6的python源代码:

import numpy as np
import matplotlib.pyplot as plt

# Set the format of labels
def LabelFormat(plt):
    ax = plt.gca()
    plt.tick_params(labelsize=14)
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    font = {'family': 'Times New Roman',
            'weight': 'normal',
            'size': 16,
            }
    return font

x = np.linspace(0, 4, 30).reshape(30, 1)
y=(x-2)**2/2

plt.figure()
plt.plot(x,y,'k-')
plt.plot(3.5,1.5**2/2,'ro')
plt.annotate('$\\frac{dE}{dx}$', xy=(3.5, 1.5**2/2), xycoords='data',
             xytext=(-60, -125), textcoords='offset points',color='r', fontsize=14, arrowprops=dict(arrowstyle="<-",
             connectionstyle="arc,rad=90", color='r'))

plt.plot(0.5,1.5**2/2,'ro')
plt.annotate('$\\frac{dE}{dx}$', xy=(0.5, 1.5**2/2), xycoords='data',
             xytext=(48, -125), textcoords='offset points',color='r', fontsize=14, arrowprops=dict(arrowstyle="<-",
             connectionstyle="arc,rad=90", color='r'))

plt.annotate('$\hat y=\\frac{1}{2}(x-2)^2$', xy=(0.25, 1.75**2/2), xycoords='data',
             xytext=(108, 0), textcoords='offset points',color='k', fontsize=14, arrowprops=dict(arrowstyle="<-",
             connectionstyle="arc,rad=90", color='w'))
# Set the labels
font = LabelFormat(plt)
plt.xlabel('$x$', font)
plt.ylabel('$\hat y$', font)
plt.show()

# To plot figure 6
x1 = np.linspace(0, 5/4.0*np.pi, 50).reshape(50, 1)
y1=np.cos(x1)

x2 = np.linspace(5/4.0*np.pi, 8, 50).reshape(50, 1)
y2=0.5*np.cos(2*x2+1*np.pi)-0.71

plt.figure()
plt.plot(x1,y1,'k-')
plt.plot(x2,y2,'k-')
plt.plot(np.pi,-1,'ro')
plt.annotate('Local optimal', xy=(np.pi, -1), xycoords='data',
             xytext=(-48, 125), textcoords='offset points',color='r', fontsize=14, arrowprops=dict(arrowstyle="->",
             connectionstyle="arc,rad=90", color='r'))

plt.plot(np.pi*2,-1.21,'ro')
plt.annotate('Global optimal', xy=(2*np.pi, -1.21), xycoords='data',
             xytext=(-48, 125), textcoords='offset points',color='r', fontsize=14, arrowprops=dict(arrowstyle="->",
             connectionstyle="arc,rad=90", color='r'))

# Set the labels
font = LabelFormat(plt)
plt.xlabel('$x$', font)
plt.ylabel('$\hat y$', font)
plt.show()

图7和图11的python源代码:

# -*- coding: utf-8 -*-
# @Time : 2020/4/7 11:28
# @Author : tengweitw

import numpy as np
from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import preprocessing


def Linear_regression_normal_equation(train_data, train_target, test_data, test_target):
    # the 1st column is 1 i.e., x_0=1
    temp = np.ones([np.size(train_data, 0), 1])
    # X is a 500*(1+2)-dim matrix
    X = np.concatenate((temp, train_data), axis=1)

    # Normal equation
    w_bar = np.matmul(np.linalg.inv(np.matmul(X.T, X)), np.matmul(X.T, train_target))

    # Training Error
    y_predict_train = np.matmul(X, w_bar)
    E_train = np.linalg.norm(y_predict_train - train_target)/len(y_predict_train)

    # Predicting
    x0 = np.ones((np.size(test_data, 0), 1))
    test_data1 = np.concatenate((x0, test_data), axis=1)
    y_predict_test = np.matmul(test_data1, w_bar)

    # Prediction Error
    E_test = np.linalg.norm(y_predict_test - test_target)/len(y_predict_test)

    return y_predict_test, E_train, E_test


def Linear_regression_normal_equation_scale(train_data, train_target, test_data, test_target):
    # Data processing: scaling
    # For training data
    ss = preprocessing.StandardScaler()
    ss.partial_fit(train_data)
    train_data_scale = ss.fit_transform(train_data)
    # For testing data
    ss.partial_fit(test_data)
    test_data_scale = ss.fit_transform(test_data)

    # the 1st column is 1 i.e., x_0=1
    temp = np.ones([np.size(train_data_scale, 0), 1])
    # X is a 500*(1+2)-dim matrix
    X = np.concatenate((temp, train_data_scale), axis=1)

    # Normal equation
    w_bar = np.matmul(np.linalg.inv(np.matmul(X.T, X)), np.matmul(X.T, train_target))

    # Training Error
    y_predict_train = np.matmul(X, w_bar)
    E_train = np.linalg.norm(y_predict_train - train_target) / len(y_predict_train)

    # Predicting
    x0 = np.ones((np.size(test_data_scale, 0), 1))
    test_data1 = np.concatenate((x0, test_data_scale), axis=1)
    y_predict_test = np.matmul(test_data1, w_bar)

    # Prediction Error
    E_test = np.linalg.norm(y_predict_test - test_target) / len(y_predict_test)

    return y_predict_test, E_train, E_test


def Linear_regression_gradient_descend(train_data, train_target, test_data, test_target):
    # learning rate
    eta = 5e-6
    M = np.size(train_data, 1)
    N = np.size(train_data, 0)
    w_bar = np.zeros((M + 1, 1))

    # the 1st column is 1 i.e., x_0=1
    temp = np.ones([N, 1])
    # X is a N*(1+M)-dim matrix
    X = np.concatenate((temp, train_data), axis=1)
    train_target = np.mat(train_target).T

    iter = 0
    num_iter = 5000
    E_train = np.zeros((num_iter, 1))

    while iter < num_iter:
        temp = np.matmul(X, w_bar) - train_target
        w_bar = w_bar - eta * np.matmul(X.T, temp)
        # Predicting training data
        y_predict_train = np.matmul(X, w_bar)
        # Training Error
        E_train[iter]=np.linalg.norm(y_predict_train - train_target)/len(y_predict_train)
        iter += 1

    # Predicting
    x0 = np.ones((np.size(test_data, 0), 1))
    test_data1 = np.concatenate((x0, test_data), axis=1)
    y_predict_test = np.matmul(test_data1, w_bar)

    # Prediction Error
    E_test = np.linalg.norm(y_predict_test.ravel()- test_target)/len(y_predict_test)

    return y_predict_test, E_train, E_test

def Linear_regression_gradient_descend_scale(train_data, train_target, test_data, test_target):
    # Data processing: scaling
    # For training data
    ss = preprocessing.StandardScaler()
    ss.partial_fit(train_data)
    train_data_scale = ss.fit_transform(train_data)
    # For testing data
    ss.partial_fit(test_data)
    test_data_scale = ss.fit_transform(test_data)

    # learning rate
    eta = 1e-3
    M = np.size(train_data_scale, 1)
    N = np.size(train_data_scale, 0)
    w_bar = np.zeros((M + 1, 1))

    # the 1st column is 1 i.e., x_0=1
    temp = np.ones([N, 1])
    # X is a N*(1+M)-dim matrix
    X = np.concatenate((temp, train_data_scale), axis=1)
    train_target = np.mat(train_target).T

    iter = 0
    num_iter = 10
    E_train = np.zeros((num_iter, 1))

    while iter < num_iter:
        temp = np.matmul(X, w_bar) - train_target
        w_bar = w_bar - eta * np.matmul(X.T, temp)
        # Predicting training data
        y_predict_train = np.matmul(X, w_bar)
        # Training Error
        E_train[iter]=np.linalg.norm(y_predict_train - train_target)/len(y_predict_train)
        iter += 1
    # Predicting
    x0 = np.ones((np.size(test_data_scale, 0), 1))
    test_data1 = np.concatenate((x0, test_data_scale), axis=1)
    y_predict_test = np.matmul(test_data1, w_bar)

    # Prediction Error
    E_test = np.linalg.norm(y_predict_test.ravel()- test_target)/len(y_predict_test)

    return y_predict_test, E_train, E_test


# Set the format of labels
def LabelFormat(plt):
    ax = plt.gca()
    plt.tick_params(labelsize=14)
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    font = {'family': 'Times New Roman',
            'weight': 'normal',
            'size': 16,
            }
    return font

def Plot_error_vs_omega(train_data,train_target):
    # ---------Show the contour of E with respect to omegas---------------------
    x1 = train_data[:, 0]
    x2 = train_data[:, 1]
    omega_1 = np.linspace(-30, 30, 30)
    omega_2 = np.linspace(-30, 30, 30)

    Y_hat = np.zeros((len(omega_1),len( omega_2)))
    for i in range(len(omega_1)):
        for j in range(len(omega_2)):
            for k in range(len(train_data)):
                temp=train_target[k] - (omega_1[i] * x1[k] + omega_2[j] * x2[k])
                Y_hat[i][j] = Y_hat[i][j] + np.square(temp)

    fig = plt.figure()

    plt.contour(omega_2,omega_1,Y_hat,20)
    # Set the labels
    font = LabelFormat(plt)
    plt.xlabel('$\omega_1$', font)
    plt.ylabel('$\omega_2$', font)

    plt.show()

def Plot_error_vs_omega_scale(train_data, train_target):
    # ---------Show the contour of E with respect to omegas---------------------
    # Data processing: scaling
    # For training data
    ss = preprocessing.StandardScaler()
    ss.partial_fit(train_data)
    train_data_scale = ss.fit_transform(train_data)

    x1 = train_data_scale[:, 0]
    x2 = train_data_scale[:, 1]
    omega_1 = np.linspace(-30, 30, 30)
    omega_2 = np.linspace(-30, 30, 30)

    Y_hat = np.zeros((len(omega_1), len(omega_2)))
    for i in range(len(omega_1)):
        for j in range(len(omega_2)):
            for k in range(len(train_data_scale)):
                temp = train_target[k] - (omega_1[i] * x1[k] + omega_2[j] * x2[k])
                Y_hat[i][j] = Y_hat[i][j] + np.square(temp)

    fig = plt.figure()

    plt.contour(omega_2, omega_1, Y_hat, 20)
    # Set the labels
    font = LabelFormat(plt)
    plt.xlabel('$\omega_1$', font)
    plt.ylabel('$\omega_2$', font)

    plt.show()


if __name__ == '__main__':

    # load house price of Boston
    data, target = load_boston(return_X_y=True)
    # The number of selected features
    M = 2
    # The first 500 data for training
    train_data = data[0:500, 0:0 + M]
    train_target = target[0:500]
    train_target.reshape(len(train_data), 1)

    # ------------------------------
    # The last 6 data for testing
    test_data = data[500:, 0:0 + M]
    test_target = target[500:]

    # To show the contour of error function E with respect to omega
    # We can see that it's a convex function, not easy for gradient descend
    Plot_error_vs_omega(train_data, train_target)
    Plot_error_vs_omega_scale(train_data, train_target)

    #---------------------------------#
    y_predict_normal_equation, E_train,E_test = Linear_regression_normal_equation(train_data, train_target, test_data,
                                                                         test_target)
    print("Linear Regression Using Normal Equation: E_train=%f, E_test=%f" % (E_train,E_test))
    for i in range(len(test_data)):
        print("True value: %f    Predicted value: %f" % (test_target[i], y_predict_normal_equation[i]))


    # ---------------------------------#
    y_predict_normal_equation_scale, E_train,E_test = Linear_regression_normal_equation_scale(train_data, train_target,
                                                                                     test_data, test_target)
    print("Linear Regression Using Normal Equation with scaling: E_train=%f, E_test=%f" % (E_train,E_test))
    for i in range(len(test_data)):
        print("True value: %f    Predicted value: %f" % (test_target[i], y_predict_normal_equation_scale[i]))


    # ---------------------------------#
    y_predict_gradient_descent, E_train,E_test = Linear_regression_gradient_descend(train_data, train_target, test_data,
                                                                           test_target)
    print("Linear Regression Using Gradient Descend: E_train=%f, E_test=%f" % (E_train[-1],E_test))
    for i in range(len(test_data)):
        print("True value: %f    Predicted value: %f" % (test_target[i], y_predict_gradient_descent[i]))

    plt.figure()
    plt.plot(E_train,'r-')
    # Set the labels
    font = LabelFormat(plt)
    plt.xlabel('Iteration', font)
    plt.ylabel('Average error: $E/N$', font)
    plt.show()


    # ---------------------------------#
    y_predict_gradient_descent_scale, E_train,E_test = Linear_regression_gradient_descend_scale(train_data, train_target,
                                                                                       test_data, test_target)
    print("Linear Regression Using Gradient Descend with scaling: E_train=%f, E_test=%f" % (E_train[-1],E_test))
    for i in range(len(test_data)):
        print("True value: %f    Predicted value: %f" % (test_target[i], y_predict_gradient_descent_scale[i]))
    plt.figure()
    plt.plot(E_train,'r-')
    # Set the labels
    font = LabelFormat(plt)
    plt.xlabel('Iteration', font)
    plt.ylabel('Average error: $E/N$', font)

    plt.show()