kNN (k-nearest neighbor)的定义
针对一个测试实例,在给定训练集中,基于某种距离度量找到与之最近的k个实例点,然后基于这k个最邻近实例点的信息,以某种决策规则来对该测试实例进行分类或回归。
由定义可知,$kNN$模型包含三个基本要素:距离度量、k值选择以及决策规则。再详细描述这三要素之前,我们先用一个样图来简单描述$kNN$分类模型的效果。
我们以二维平面为例,假设输入的训练集格式为$(x_1,x_2,l)$,其中$x_1, x_2$为横纵坐标,$l$为标签。这里我们考虑$k=1,3$的情况,决策规则为多数投票规则,即测试实例与k个实例中的多数属于同一类。图$1,2$分别是$k=1,3$时,二维特征空间划分图。
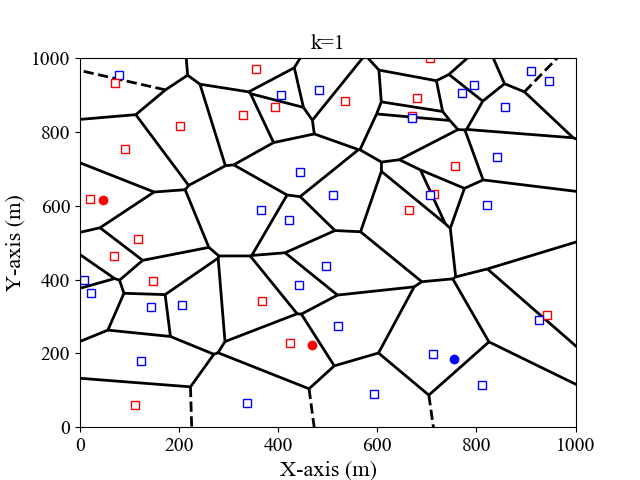
距离度量
$kNN$的本质是“近朱者赤近墨者黑”,即测试点的类别由其最邻近的$k$个实例点决定。这里“最邻近”的意义根据距离度量的不同而不同。一般来说,我们最常见的便是欧氏距离。这里我们介绍包含欧氏距离,但比欧氏距离更普适的Minkowski距离。
假定训练集中,每个实例包含$n$个特征,那么实例$x$可以分别表示为$x=(x_1,\cdots,x_n)$。假定测试实例为$y=(y_1,\cdots,y_n)$,那么$x, y$之间的Minkowski距离可以表示为:
其中,$p>0$是一个可变参数:
当然$p$也可以取小于$1$的值,如$p=\frac{1}{2}$。图$3$给出了当$p$取不同值时,与原点距离为$1$的图形:
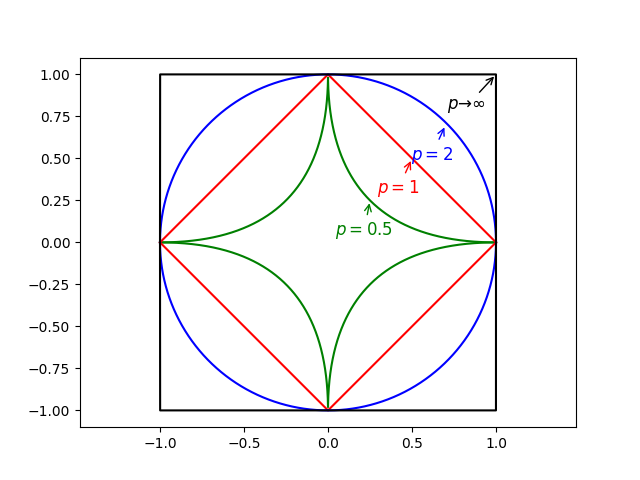
Note: 这里只是介绍了较常用的Minkowski距离,
$k$值的选择
调参是机器学习算法的重要一环。在$kNN$算法中,$k$值的选取对结果的影响较大。下面以图$4$来具体说明:
(a)当$k$取值较小时,此时是根据测试实例周围较少的训练样例信息来进行分类。由于训练样例离测试样例比较近,因此训练误差比较小。当这些邻近的训练样例是噪声时,会严重影响分类结果,即泛化误差变大。
(b)当$k$取值较大时,此时是根据测试实例周围较多的训练样例信息来进行分类。这时与测试实例相距较远(相关性较小)的训练样例也对分类结果有影响,使得泛化误差较大。一个极端的例子就是以考虑所有的训练样例,这时测试样例被归为训练样例数最大的一类。
Note: 模型复杂度的理解:对于有参模型来说(例如线性拟合),模型复杂度一般可以用参数的多少来判断。对于无参模型来说(例如这里的$kNN$),这里还需思考。可能的情况?考虑极端情况,当$k$取值为整个训练样例数时,这时的模型最简单,即测试样例被归为训练样例数最大的一类。当$k$取值为$1$时,每个测试样例都需要根据其最邻近节点来进行分类,这时模型变得很复杂。
通常来说,我们可以通过交叉验证来选取$k$值。同时,我们也可以对这$k$个训练样例进行距离加权,来克服(b)的影响。
决策规则
$kNN$既可进行分类,也可用于回归。
- 对于分类问题来说,一般采用的是投票法,即测试样例被归为最邻近$k$个训练样例数中最大的一类。
- 对于回归问题来说,一般采用的是平均法。顾名思义,测试样例的取值为这$k$个训练样例取值的平均值。
- 最后,我们可以对这两种方法进行改进,即对这$k$个训练样例进行加权,离测试样例较近的训练样例一般具有更大的影响权重。
$kNN$优缺点:
优点:
最近更新于20-01-20,明早就回家过年了,年后再更新。
未完待续。。。
最近更新于20-03-30,优缺点还需用图示说明。
算法实践
下面我们给出两种方式实现KNN分类算法:一、自己编程实现KNN算法;二、使用更加简单的scikit-learn库。
注意:数据集为iris数据集,有150个训练集,4个feature, 总共分3类。在方法一中,我们考虑了所有4个feature,将所有150个训练数据作为训练(即在程序中设置split=1),读者可以通过设置split的值来获取测试集用于交叉检验得到最佳的k值。在方法二中,我们只考虑了前2个feature,这么做是为了在二维图中展示分类结果。
自写KNN算法
- 算法思路:
- 计算已知数据集中的点与当前点之间的距离
- 按照距离递增次序进行排序
- 选取与当前点距离最小的K个点
- 确定这K个点所在类别的出现次数
- 返回这K个点出现次数最多的类别作为当前点的预测分类
- 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60from sklearn import datasets, neighbors
import random
import math
import numpy as np
# Divide the original dataset into training data and test data
def LoadDataSet(irisData, split, trainData, testData, trainLabel, testLabel):
allData = irisData.data
allLabel = irisData.target
for i in range(len(allData)):
if random.random() < split: #
trainData.append(allData[i])
trainLabel.append(allLabel[i])
else:
testData.append(allData[i])
testLabel.append(allLabel[i])
# Calculate the distance between two instance
def CalDist(instance1, instance2):
dist = 0
length = len(instance1)
for i in range(length):
dist += pow((instance1[i] - instance2[i]), 2)
return math.sqrt(dist)
# The KNN algorithm
def knn(instance, k, trainData, trainLabel):
allDist = []
# Calculate distances from all training data
for i in range(len(trainData)):
allDist.append([CalDist(instance, trainData[i]), i])
allDist.sort()
# Determine the neighbors
neighbors = []
for j in range(k):
neighbors.append(allDist[j][1])
numLabels = len(np.unique(trainLabel))
vote = [0] * numLabels
# Vote to decide the resultant label
for kk in range(k):
vote[trainLabel[neighbors[kk]]] += 1
# print the result
print(vote.index(max(vote)))
# load dataset of iris
irisData = datasets.load_iris()
# All data are used for training
split = 1
# Number of neighbors
k = 3
trainData = []
trainLabel = []
testData = []
testLabel = []
LoadDataSet(irisData, split, trainData, testData, trainLabel, testLabel)
predictPoint=[7.6, 3., 6.6, 2.1]
knn(predictPoint, k, trainData, trainLabel)
使用scikit-learn库
- 代码实现
1 | import numpy as np |
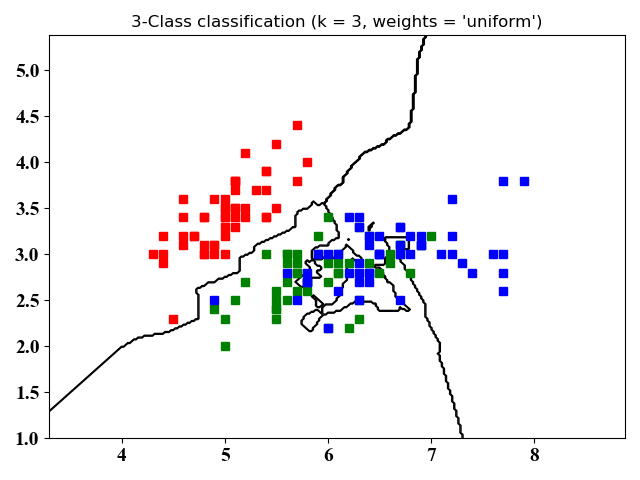
- 仿真结果
图4和图5没有本质区别,不同之处在于图4只画了分类的轮廓,图5是将整个空间的点进行了分类。从图中可以看出,kNN适合于非线性分类。
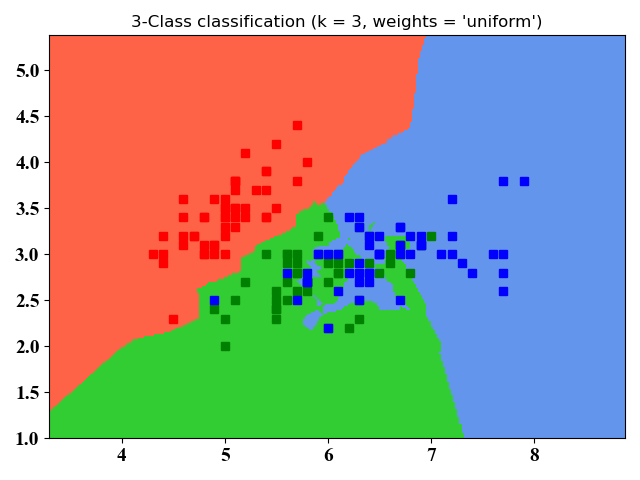
附录
图1的python 源代码:
1 | import numpy as np |
图3的python源代码:
1 | import numpy as np |

