【算法导论】动态规划之矩阵链乘法

​ 所谓矩阵链乘法是指当一些矩阵相乘时，如何加括号来改变乘法顺序从而来降低乘法次数。例如有三个矩阵连乘：$A_1\cdot A_2\cdot A_3$，其维数分别为：$10\times 100$，$100\times 5$，$5\times 50$. 如果按照$((A_1\cdot A_2)\cdot A_3)$来计算的话，求$(A_1\cdot A_2)$要$10\cdot 100\cdot 5=5000$次乘法，再乘以$A_3$需要$10\cdot 5\cdot 50=2500$次乘法，因此总共需要$7500$次乘法。如果按照$(A_1\cdot (A_2\cdot A_3))$来计算的话，求$(A_2\cdot A_3)$要$100\cdot 5\cdot 50=25000$次乘法，再乘以$A_1$需要$10\cdot 100\cdot 50=50000$次乘法，因此总共需要$75000$次乘法。可见，按不同的顺序计算，代价相差很大。

​ 矩阵链乘法问题可以表述如下：给定$n$个矩阵构成的一个链$(A_1\cdot A_2\cdot A_3\cdot\ldots\cdot A_n)$，其中$i=1,2,……n$，矩阵$A_i$的维数为$p(i-1)\cdot p(i)$，对于乘积$A_1\cdot A_2\cdot A_3\cdot\ldots\cdot A_n$以一种最小化标量乘法次数的方式进行加括号。

​ 解决这个问题，我们可以用穷举法，但是$n$很大时，这不是个好方法，其时间复杂度为指数形式。拿上面的例子来说，加括号后把矩阵链分成了两部分，计算代价为两者代价的和。因此假设这种方法的代价最少，则两个部分的代价也是最小的，如果不是最小的，那么这种方法就不是最优的，因此矩阵链乘法具有最优子结构。因此我们可以利用子问题的最优解来构造原问题的一个最优解。所以，可以把问题分割为两个子问题$(A1\cdot A_2\cdot A_3\cdot\ldots\cdot A_k$和$A{k+1}\cdot A{k+2}\cdot A{k+3}\cdot\ldots\cdot A_n)$,需找子问题的最优解，然后合并这些问题的最优解。从下面的程序可以看出，其时间复杂度为$O(n^3)$.

上面算法的实现程序如下：

#include<stdio.h>

void print_parens(int s[6][6],int i ,int j);//打印加括号的位置
void matrix_order(int *p,int n,int m[6][6],int s[6][6]);//计算最佳的加括号的方式
void main()
{
	int p[7]={30,35,15,5,10,20,25};//记录6个矩阵的行和列，注意相邻矩阵的行和列是相同的
	int m[6][6]={0};//存储第i个矩阵到第j个矩阵的计算代价（以乘法次数来表示）
	int s[6][6]={0};//存储第i个矩阵到第j个矩阵的最小代价时的分为两部分的位置
	int n=6;//矩阵个数
	matrix_order(p,n,m,s);
	printf("最终加括号的形式为： ");
	print_parens(s,0 ,5);//计算从第1个矩阵到第6个矩阵的最优加括号的方法
	printf("\n");
  
}
/****************************************************\
函数功能：计算最佳的加括号的方式，得到m和s矩阵
输入：    矩阵的行和列p,初始化的m和s矩阵
输出：    无
\****************************************************/
void matrix_order(int *p,int n,int m[6][6],int s[6][6])
{
	int q=0;
	int j=0;
	for(int i=0;i<n;i++)
		m[i][i]=0;
	for(int l=2;l<=n;l++)
		for(int i=0;i<n-l+1;i++)
		{
			j=i+l-1;
			m[i][j]=1000000;
			for(int k=i;k<j;k++)//在i,j中遍历每一个分割的位置
			{
				q=m[i][k]+m[k+1][j]+p[i]*p[k+1]*p[j+1];//计算代价
				if(q<m[i][j])
				{
					m[i][j]=q;
					s[i][j]=k;
				}

			}
		}
}


/****************************************************\
函数功能：打印加括号的位置
输入：    s矩阵，想要计算的矩阵链的起始和结尾位置
输出：    无
\****************************************************/
void print_parens(int s[6][6],int i ,int j)
{
	if(i==j)
		printf("A%d",i);
	else
	{
		printf("(");
		print_parens(s,i,s[i][j]);
		print_parens(s,s[i][j]+1,j);//递归调用
		printf(")");
	}
	
}

在上面程序的实现中，矩阵链的参数如下表：

matrix	dimension
$A_1$	30 × 35
$A_2$	35 × 15
$A_3$	15 × 5
$A_4$	5 × 10
$A_5$	10 × 20
$A_6$	20 × 25

表示第$i$个矩阵到第$j$个矩阵的计算代价矩阵$m[i][j]$和表示第$i$个矩阵到第$j$个矩阵的最小代价时的分为两部分的位置矩阵$s[i][j]$的结果如下图：

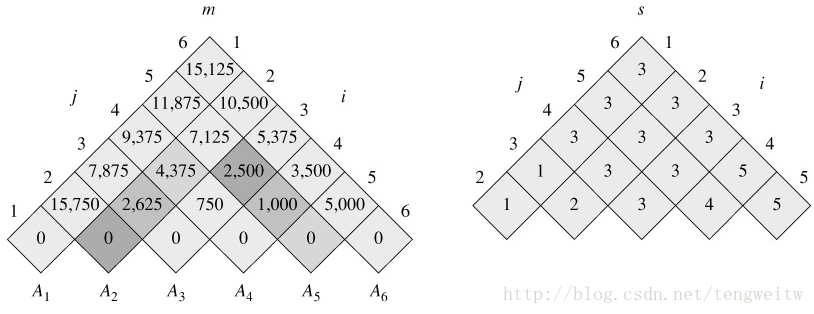
从上面左图的$m$矩阵可以看出任意第$i$个到第$j$个矩阵连乘的乘法次数。最终的加括号形式为：$(A_1(A_2A_3))((A_4A_5)A_6)$

用动态规划算法解矩阵链乘法问题需要时间为$O(n^3)$，空间为$O(n^2)$，这比采用穷举法的指数时间相比要有效的多。